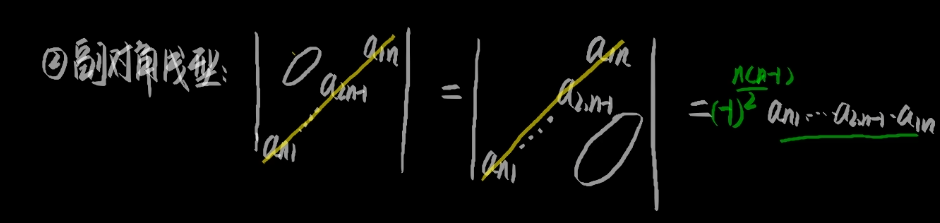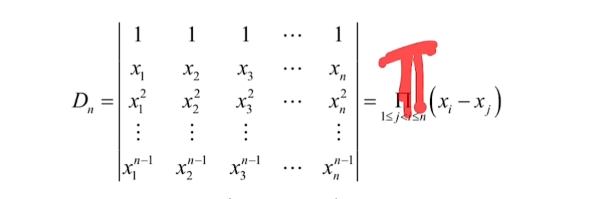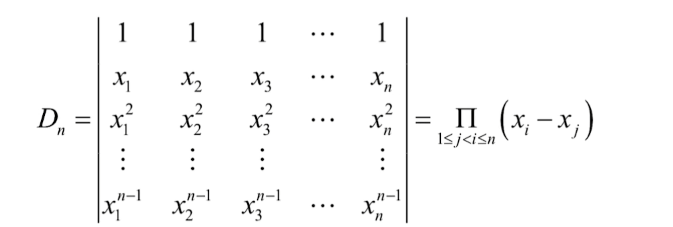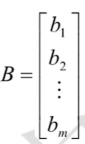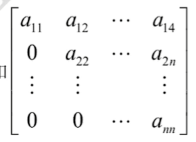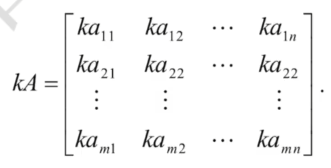线性代数 行列式 行列式书写形式D 3 = ∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ D_3=\begin{vmatrix}a_{11}&a_{12} &a_{13} \\a_{21}&a_{22} &a_{23} \\a_{31} &a_{32} &a_{33}\end{vmatrix} D 3 = ∣ ∣ ∣ ∣ ∣ ∣ ∣ a 1 1 a 2 1 a 3 1 a 1 2 a 2 2 a 3 2 a 1 3 a 2 3 a 3 3 ∣ ∣ ∣ ∣ ∣ ∣ ∣
行列式的计算 本质上的计算:D n = ∣ a 11 … a 1 n ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ a n 1 ⋅ ⋅ ⋅ a n n ∣ D_n=\begin{vmatrix}a_{11} &… & a_{1n}\\··· & ··· &··· \\a_{n1} &··· &a_{nn}\end{vmatrix} D n = ∣ ∣ ∣ ∣ ∣ ∣ ∣ a 1 1 ⋅ ⋅ ⋅ a n 1 … ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ a 1 n ⋅ ⋅ ⋅ a n n ∣ ∣ ∣ ∣ ∣ ∣ ∣
对角线法则 仅适用于二阶到三阶的行列式计算
二阶行列式 D 2 = ∣ a b c d ∣ = a d − c b D_2=\begin{vmatrix}a &b \\c &d\end{vmatrix}=ad-cb D 2 = ∣ ∣ ∣ ∣ ∣ a c b d ∣ ∣ ∣ ∣ ∣ = a d − c b
三阶行列式 D 3 = ∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 − a 13 a 22 a 31 − a 12 a 21 a 33 − a 11 a 23 a 32 D_3=\begin{vmatrix}a_{11} &a_{12} &a_{13} \\a_{21} &a_{22} &a_{23} \\a_{31} &a_{32} &a_{33}\end{vmatrix}=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32} D 3 = ∣ ∣ ∣ ∣ ∣ ∣ ∣ a 1 1 a 2 1 a 3 1 a 1 2 a 2 2 a 3 2 a 1 3 a 2 3 a 3 3 ∣ ∣ ∣ ∣ ∣ ∣ ∣ = a 1 1 a 2 2 a 3 3 + a 1 2 a 2 3 a 3 1 + a 1 3 a 2 1 a 3 2 − a 1 3 a 2 2 a 3 1 − a 1 2 a 2 1 a 3 3 − a 1 1 a 2 3 a 3 2 ∣ 1 1 − 5 − 2 2 2 1 − 1 0 ∣ \begin{vmatrix}1&1&-5\\-2&2&2\\1&-1&0\end{vmatrix} ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 − 2 1 1 2 − 1 − 5 2 0 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 1 − 5 − 2 2 2 1 − 1 0 ∣ 1 1 − 2 2 1 − 1 \begin{vmatrix}1&1&-5\\-2&2&2\\1&-1&0\end{vmatrix}{\color{Red} \begin{matrix}1&1\\-2&2\\1&-1\end{matrix}} ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 − 2 1 1 2 − 1 − 5 2 0 ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 − 2 1 1 2 − 1 1 ∗ 2 ∗ 0 + 1 ∗ 2 ∗ 1 + ( − 5 ) ∗ ( − 2 ) ∗ ( − 1 ) − ( − 5 ) ∗ 2 ∗ 1 − 1 ∗ 2 ∗ ( − 1 ) − 1 ∗ ( − 2 ) ∗ 0 1*2*0+1*2*1+(-5)*(-2)*(-1)-(-5)*2*1-1*2*(-1)-1*(-2)*0 1 ∗ 2 ∗ 0 + 1 ∗ 2 ∗ 1 + ( − 5 ) ∗ ( − 2 ) ∗ ( − 1 ) − ( − 5 ) ∗ 2 ∗ 1 − 1 ∗ 2 ∗ ( − 1 ) − 1 ∗ ( − 2 ) ∗ 0 = 0 + 2 − 10 + 10 + 2 − 0 = 4 =0+2-10+10+2-0=4 = 0 + 2 − 1 0 + 1 0 + 2 − 0 = 4 ∣ 1 1 1 1 2 x 1 4 x 2 ∣ = 0 \begin{vmatrix}1&1&1\\1&2&x\\1&4&x^2\end{vmatrix}=0 ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 1 1 1 2 4 1 x x 2 ∣ ∣ ∣ ∣ ∣ ∣ ∣ = 0 ∣ 1 1 1 1 2 x 1 4 x 2 ∣ 1 1 1 2 1 4 \begin{vmatrix}1&1&1\\1&2&x\\1&4&x^2\end{vmatrix}{\color{Red} \begin{matrix}1&1\\1&2\\1&4\end{matrix}} ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 1 1 1 2 4 1 x x 2 ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 1 1 1 2 4 1 ∗ 2 ∗ x + 1 ∗ x ∗ 1 + 1 ∗ 1 ∗ 4 − ( 4 ∗ x ∗ 1 + x 2 ∗ 1 ∗ 1 ) = 0 1*2*x+1*x*1+1*1*4-(4*x*1+x^2*1*1)=0 1 ∗ 2 ∗ x + 1 ∗ x ∗ 1 + 1 ∗ 1 ∗ 4 − ( 4 ∗ x ∗ 1 + x 2 ∗ 1 ∗ 1 ) = 0 x 2 − 3 x + 2 = 0 x^2-3x+2=0 x 2 − 3 x + 2 = 0 ( x − 1 ) ( x − 2 ) = 0 (x-1)(x-2)=0 ( x − 1 ) ( x − 2 ) = 0 x 1 = 1 , x 2 = 2 x_1=1,x_2=2 x 1 = 1 , x 2 = 2
克拉默法则计算方程组 例如:{ 3 x 1 − 2 x 2 = 12 2 x 1 + x 2 = 1 \left\{\begin{matrix}3x_1-2x_2=12 \\2x_1+x_2=1\end{matrix}\right. { 3 x 1 − 2 x 2 = 1 2 2 x 1 + x 2 = 1 x 1 , x 2 x_1,x_2 x 1 , x 2 D = ∣ 3 − 2 2 1 ∣ D=\begin{vmatrix}3&-2\\2&1\end{vmatrix} D = ∣ ∣ ∣ ∣ ∣ 3 2 − 2 1 ∣ ∣ ∣ ∣ ∣ x 1 = ∣ 12 − 2 1 1 ∣ D = 2 x_1=\frac{\begin{vmatrix}12&-2\\1&1\end{vmatrix}}{D}=2 x 1 = D ∣ ∣ ∣ ∣ 1 2 1 − 2 1 ∣ ∣ ∣ ∣ = 2 x 2 = ∣ 12 3 1 2 ∣ D = − 3 x_2=\frac{\begin{vmatrix}12&3\\1&2\end{vmatrix}}{D}=-3 x 2 = D ∣ ∣ ∣ ∣ 1 2 1 3 2 ∣ ∣ ∣ ∣ = − 3
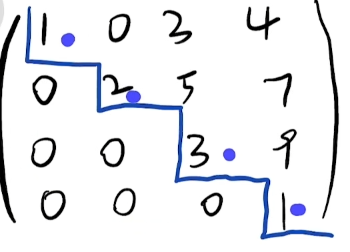
化三角形行列式 主对角类型:D n = ∣ a 11 0 0 0 a 22 0 0 0 a 33 ∣ = a 11 a 22 a 33 D_n=\begin{vmatrix}a_{11} &0 &0 \\0 &a_{22} &0 \\0 &0 &a_{33}\end{vmatrix}=a_{11}a_{22}a_{33} D n = ∣ ∣ ∣ ∣ ∣ ∣ ∣ a 1 1 0 0 0 a 2 2 0 0 0 a 3 3 ∣ ∣ ∣ ∣ ∣ ∣ ∣ = a 1 1 a 2 2 a 3 3 D n = ∣ 0 0 a 13 0 a 22 0 a 31 0 0 ∣ = ( − 1 n ( n − 1 ) 2 ) a 13 a 22 a 31 D_n=\begin{vmatrix}0 &0 &a_{13} \\0 &a_{22} &0 \\a_{31} &0 &0\end{vmatrix}=(-1^{\frac{n(n-1)}{2} })a_{13}a_{22}a_{31} D n = ∣ ∣ ∣ ∣ ∣ ∣ ∣ 0 0 a 3 1 0 a 2 2 0 a 1 3 0 0 ∣ ∣ ∣ ∣ ∣ ∣ ∣ = ( − 1 2 n ( n − 1 ) ) a 1 3 a 2 2 a 3 1 ∣ 1 2 3 0 2 1 0 0 3 ∣ \begin{vmatrix}1&2&3\\0&2&1\\0&0&3\end{vmatrix} ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 0 0 2 2 0 3 1 3 ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 ∗ 2 ∗ 3 = 6 1*2*3=6 1 ∗ 2 ∗ 3 = 6 lim n → ∞ ∣ 1 2 − 1 2 0 1 3 1 0 0 − 1 4 ∣ n \lim_{n \to \infty}\begin{vmatrix}\frac{1}{2}&-1&2\\0&\frac{1}{3} &1\\0&0&-\frac{1}{4} \end{vmatrix}^n lim n → ∞ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 2 1 0 0 − 1 3 1 0 2 1 − 4 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ n lim n → ∞ ( 1 2 ∗ 1 3 ∗ ( − 1 4 ) ) n \lim_{n \to \infty}(\frac{1}{2}*\frac{1}{3}*(-\frac{1}{4}) )^n lim n → ∞ ( 2 1 ∗ 3 1 ∗ ( − 4 1 ) ) n lim n → ∞ ( − 1 24 ) n \lim_{n \to \infty}(-\frac{1}{24})^n lim n → ∞ ( − 2 4 1 ) n lim n → ∞ − 1 n 2 4 n \lim_{n \to \infty}\frac{-1^n}{24^n} lim n → ∞ 2 4 n − 1 n lim n → ∞ 1 ∞ = 0 \lim_{n \to \infty}\frac{1}{\infty}=0 lim n → ∞ ∞ 1 = 0
转置行列式 对行列式中的行与列进行转换 、D = ∣ 1 3 5 2 4 8 7 6 9 ∣ ⇒ D T = ∣ 1 2 7 3 4 6 5 8 9 ∣ D=\begin{vmatrix}1&3&5\\2&4&8\\7&6&9\end{vmatrix}\Rightarrow D^T=\begin{vmatrix}1&2&7\\3&4&6\\5&8&9\end{vmatrix} D = ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 2 7 3 4 6 5 8 9 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ⇒ D T = ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 3 5 2 4 8 7 6 9 ∣ ∣ ∣ ∣ ∣ ∣ ∣
行列式的性质
行列式和它的转置行列式相等;即D T = D D^T=D D T = D
(互换) :交换行列式某两行(列),行列式变号; (倍乘) :行列式的某行(列)的所以元素的公因子都可以提到行列式符号的外面; (倍加) :将行列式的某一行(列)各元素的k k k 若行列式某一行(列)的元素是两个数之和,则行列式等于两个行列式之和;
求解行(列)和相 等行列式 每一行或者每一列加起来的和相等的行列式;构造三角形行列式的技巧 :a. 先找”1” ; b. 按列用“1”化0;∣ 1 + a 1 1 1 2 2 + a 2 2 3 3 3 + a 3 4 4 4 4 + a ∣ \begin{vmatrix}1+a&1&1&1\\2&2+a&2&2\\3&3&3+a&3\\4&4&4&4+a\end{vmatrix} ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 + a 2 3 4 1 2 + a 3 4 1 2 3 + a 4 1 2 3 4 + a ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ D = r 1 + r i i = 2 , 3 , 4 = 10 + a 10 + a 10 + a 10 + a 2 2 + a 2 2 3 3 3 + a 3 4 4 4 4 + a D=\frac{r_1+r_i}{i=2,3,4}=\begin{matrix}10+a&10+a&10+a&10+a\\2&2+a&2&2\\3&3&3+a&3\\4&4&4&4+a\end{matrix} D = i = 2 , 3 , 4 r 1 + r i = 1 0 + a 2 3 4 1 0 + a 2 + a 3 4 1 0 + a 2 3 + a 4 1 0 + a 2 3 4 + a D = r 1 + r i i = 2 , 3 , 4 = ( 10 + a ) 1 1 1 1 2 2 + a 2 2 3 3 3 + a 3 4 4 4 4 + a D=\frac{r_1+r_i}{i=2,3,4}=(10+a)\begin{matrix}1&1&1&1\\2&2+a&2&2\\3&3&3+a&3\\4&4&4&4+a\end{matrix} D = i = 2 , 3 , 4 r 1 + r i = ( 1 0 + a ) 1 2 3 4 1 2 + a 3 4 1 2 3 + a 4 1 2 3 4 + a = r 2 + 2 r i r 3 − 3 r 1 , r 4 + 4 r 1 = ( 10 + a ) 1 1 1 1 0 a 0 0 0 0 a 0 0 0 0 a =\frac{r_2+2r_i}{r_3-3r_1,r_4+4r_1}=(10+a)\begin{matrix}1&1&1&1\\0&a&0&0\\0&0&a&0\\0&0&0&a\end{matrix} = r 3 − 3 r 1 , r 4 + 4 r 1 r 2 + 2 r i = ( 1 0 + a ) 1 0 0 0 1 a 0 0 1 0 a 0 1 0 0 a = ( 10 + a ) ( 1 ⋅ a ⋅ a ⋅ a ) = ( 10 + a ) ⋅ a 3 =(10+a)(1\cdot a \cdot a\cdot a )=(10+a)\cdot a^3 = ( 1 0 + a ) ( 1 ⋅ a ⋅ a ⋅ a ) = ( 1 0 + a ) ⋅ a 3
爪形行列式的计算 形如除一行和一列以及主对角线外都为0的行列式为爪形行列式;∣ 1 1 1 1 1 2 0 0 1 0 3 0 1 0 0 4 ∣ \begin{vmatrix}1&1&1&1\\1&2&0&0\\1&0&3&0\\1&0&0&4\end{vmatrix} ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 1 1 1 1 2 0 0 1 0 3 0 1 0 0 4 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ D = c 1 − 1 4 c 4 = 1 − 1 4 1 1 1 1 2 0 0 1 0 3 0 0 0 0 4 D=\frac{c_1-\frac{1}{4}c_4 }{}=\begin{matrix}1-\frac{1}{4}&1&1&1\\1&2&0&0\\1&0&3&0\\0&0&0&4\end{matrix} D = c 1 − 4 1 c 4 = 1 − 4 1 1 1 0 1 2 0 0 1 0 3 0 1 0 0 4 D = c 1 − 1 3 c 3 = 1 − 1 4 − 1 3 1 1 1 0 2 0 0 0 0 3 0 0 0 0 4 D=\frac{c_1-\frac{1}{3}c_3 }{}=\begin{matrix}1-\frac{1}{4}-\frac{1}{3}&1&1&1\\0&2&0&0\\0&0&3&0\\0&0&0&4\end{matrix} D = c 1 − 3 1 c 3 = 1 − 4 1 − 3 1 0 0 0 1 2 0 0 1 0 3 0 1 0 0 4 D = c 1 − 1 2 c 2 = 1 − 1 4 − 1 3 − 1 2 1 1 1 0 2 0 0 1 0 3 0 0 0 0 4 D=\frac{c_1-\frac{1}{2}c_2 }{}=\begin{matrix}1-\frac{1}{4}-\frac{1}{3}-\frac{1}{2}&1&1&1\\0&2&0&0\\1&0&3&0\\0&0&0&4\end{matrix} D = c 1 − 2 1 c 2 = 1 − 4 1 − 3 1 − 2 1 0 1 0 1 2 0 0 1 0 3 0 1 0 0 4 = ( 1 − 1 4 − 1 3 − 1 2 ) ⋅ 24 = − 2 =(1-\frac{1}{4}-\frac{1}{3}-\frac{1}{2})\cdot 24=-2 = ( 1 − 4 1 − 3 1 − 2 1 ) ⋅ 2 4 = − 2
行列式的展开定理(降阶法)
余子式
代数余子式∣ 3 1 4 8 9 5 1 1 1 ∣ \begin{vmatrix}3&1&4\\8&9&5\\1&1&1\end{vmatrix} ∣ ∣ ∣ ∣ ∣ ∣ ∣ 3 8 1 1 9 1 4 5 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ a 32 = 1 a_{32}=1 a 3 2 = 1 a 32 a_{32} a 3 2 A 32 = ( − 1 ) 3 + 2 ⋅ M 32 = − M 32 A_{32}=(-1)^{3+2}\cdot M_{32}=-M_{32} A 3 2 = ( − 1 ) 3 + 2 ⋅ M 3 2 = − M 3 2 = − ∣ 3 4 8 5 ∣ = − ( 15 − 32 ) =-\begin{vmatrix}3&4\\8&5\end{vmatrix}=-(15-32) = − ∣ ∣ ∣ ∣ ∣ 3 8 4 5 ∣ ∣ ∣ ∣ ∣ = − ( 1 5 − 3 2 ) A 32 = 17 A_{32}=17 A 3 2 = 1 7 D = ∣ 1 0 2 x 3 1 4 x 5 ∣ D=\begin{vmatrix}1&0&2\\x&3&1\\4&x&5\end{vmatrix} D = ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 x 4 0 3 x 2 1 5 ∣ ∣ ∣ ∣ ∣ ∣ ∣ A 12 = − 1 A_{12}=-1 A 1 2 = − 1 A 21 = A_{21}= A 2 1 = A 12 = ( − 1 ) 1 + 2 ⋅ M 12 = − M 12 A_{12}=(-1)^{1+2}\cdot M_{12}=-M_{12} A 1 2 = ( − 1 ) 1 + 2 ⋅ M 1 2 = − M 1 2 = − ∣ x 1 4 5 ∣ = − 5 x + 4 =-\begin{vmatrix}x&1\\4&5\end{vmatrix}=-5x+4 = − ∣ ∣ ∣ ∣ ∣ x 4 1 5 ∣ ∣ ∣ ∣ ∣ = − 5 x + 4 A 12 = − 5 x + 4 = − 1 A_{12}=-5x+4=-1 A 1 2 = − 5 x + 4 = − 1 x = 1 x=1 x = 1 A 21 = ( − 1 ) 2 + 1 ⋅ M 21 = − M 21 A_{21}=(-1)^{2+1}\cdot M_{21}=-M_{21} A 2 1 = ( − 1 ) 2 + 1 ⋅ M 2 1 = − M 2 1 = − ∣ 0 2 x 1 ∣ = − 2 x =-\begin{vmatrix}0&2\\x&1\end{vmatrix}=-2x = − ∣ ∣ ∣ ∣ ∣ 0 x 2 1 ∣ ∣ ∣ ∣ ∣ = − 2 x A 21 = ( − 1 ) ⋅ ( − 2 x ) = 2 ⋅ 1 = 2 A_{21}=(-1)\cdot (-2x)=2\cdot 1=2 A 2 1 = ( − 1 ) ⋅ ( − 2 x ) = 2 ⋅ 1 = 2
拉普拉斯展开 某一行列式:对行列式任一行(列)的各元素与对应的代数余子式乘积之和;D = a i 1 A i 1 + a i 2 A i 2 + … … + a i n A i n ( i = 1 , 2 … … n ) D=a_{i1}A_{i1}+a_{i2}A_{i2}+……+a_{in}A_{in}(i=1,2……n) D = a i 1 A i 1 + a i 2 A i 2 + … … + a i n A i n ( i = 1 , 2 … … n ) D = a 1 j A 1 j + a 2 j A 2 j + … … + a n j A n j ( j = 1 , 2 … … n ) D=a_{1j}A_{1j}+a_{2j}A_{2j}+……+a_{nj}A_{nj}(j=1,2……n) D = a 1 j A 1 j + a 2 j A 2 j + … … + a n j A n j ( j = 1 , 2 … … n )
展开的逆用 求行列式的某行(列)代数余子式相加时,则将原行列式对应行(列)换成要求代数余子式前的系数;
范德蒙行列式
矩阵 矩阵的基本概念
定义:由m × n m \times n m × n m m m n n n (行数和列数可以不相等) 称为m m m n n n A , A m × n A,A_{m \times n} A , A m × n A = ( a i j ) m × n A=(a_{ij})_{m \times n} A = ( a i j ) m × n A = ( a 1 , a 2 , … … a n ) A=(a_1,a_2,……a_n) A = ( a 1 , a 2 , … … a n ) 列矩阵 O O O 不同行或列的零矩阵不同 )行列数相同 ),记为E 、 I E、I E 、 I 单位矩阵 上三角矩阵 ,下三角矩阵反之;三角形矩阵 A = ( a i j ) A=(a_{ij}) A = ( a i j ) n n n A T = A A^T=A A T = A A T = − A A^T=-A A T = − A
性质A , B A,B A , B A + B , λ A A+B,\lambda A A + B , λ A λ \lambda λ A , B A,B A , B A B AB A B A B = B A AB=BA A B = B A
矩阵的运算
加减运算:对应元素相加减A = ( a i j ) m × n A=(a_{ij})_{m \times n} A = ( a i j ) m × n B = ( b i j ) m × n B=(b_{ij})_{m \times n} B = ( b i j ) m × n m × n m \times n m × n A ± B = ( a i j ± b i j ) m × n A \pm B =(a_{ij }\pm b_{ij})_{m \times n} A ± B = ( a i j ± b i j ) m × n 只能是同类型矩阵才可以进行加减运算且必须满足加法运算规律
矩阵的数乘:对矩阵所有元素进行数乘矩阵的数乘
矩阵的乘法A A A m × s m \times s m × s B B B s × n s \times n s × n A = ( a i j ) m × s , B = ( b i j ) s × n A=(a_{ij})_{m \times s},B=(b_{ij})_{s \times n} A = ( a i j ) m × s , B = ( b i j ) s × n A , B A,B A , B A m × s ⋅ B s × n = C m × n A_{m \times s} \cdot B_{s \times n}=C_{m \times n} A m × s ⋅ B s × n = C m × n A B = C AB=C A B = C C i j = ∑ k = 1 s a i k b k j ( i = 1 … … m , j = 1 … … n ) C_{ij}=\sum_{k=1}^{s}a_{ik}b_{kj}(i=1……m,j=1……n) C i j = ∑ k = 1 s a i k b k j ( i = 1 … … m , j = 1 … … n ) 第一个矩阵的列数和第二个矩阵的行数相同才可以乘;矩阵乘法不满足乘法交换律,但满足结合律和分配律 ( A B ) C = A ( B C ) (AB)C=A(BC) ( A B ) C = A ( B C ) k ( A B ) = ( k A ) B = A ( k B ) k(AB)=(kA)B=A(kB) k ( A B ) = ( k A ) B = A ( k B ) A ( B + C ) = A B + A C A(B+C)=AB+AC A ( B + C ) = A B + A C ( B + C ) A = B A + C A (B+C)A=BA+CA ( B + C ) A = B A + C A
矩阵的转置A A A A A A A T A^T A T 转置矩阵的运算规律: ( A T ) T = A (A^T)^T=A ( A T ) T = A ( A + B ) T = A T + B T (A+B)^T=A^T+B^T ( A + B ) T = A T + B T ( λ A ) T = λ A T (\lambda A)^T=\lambda A^T ( λ A ) T = λ A T ( A B ) T = B T A T (AB)^T=B^T A^T ( A B ) T = B T A T
方阵的行列式A A A A A A A A A ∣ A ∣ |A| ∣ A ∣ 性质1:∣ A T ∣ = ∣ A ∣ |A^T|=|A| ∣ A T ∣ = ∣ A ∣ ∣ k A ∣ = k n ∣ A ∣ |kA|=k^n|A| ∣ k A ∣ = k n ∣ A ∣ k k k ∣ A B ∣ = ∣ A ∣ ∣ B ∣ |AB|=|A||B| ∣ A B ∣ = ∣ A ∣ ∣ B ∣
矩阵的逆
定义n n n A A A n n n B B B A B = B A = E AB=BA=E A B = B A = E A A A B B B A A A A A A A − 1 A^{-1} A − 1 A B = B A = E AB=BA=E A B = B A = E B = A − 1 B=A^{-1} B = A − 1 A A A A A A
定理1A A A ∣ A ∣ ≠ 0 |A|\ne 0 ∣ A ∣ = 0
定理2∣ A ∣ ≠ 0 |A|\ne 0 ∣ A ∣ = 0 A A A A − 1 = A ∗ ∣ A ∣ A^{-1}=\frac{A^*}{|A|} A − 1 = ∣ A ∣ A ∗ A ∗ A^* A ∗ A A A 伴随矩阵 A i j A_{ij} A i j a i j a_{ij} a i j ∣ A ∣ |A| ∣ A ∣ 二阶伴随矩阵规律:主对角线元素互换,副对角线元素添加负号。
定理3A A ∗ = A ∗ ⋅ A = ∣ A ∣ E AA^*=A^* \cdot A=|A|E A A ∗ = A ∗ ⋅ A = ∣ A ∣ E
逆矩阵的性质
若A A A A − 1 A^{-1} A − 1 ( A − 1 ) − 1 = A (A^{-1})^{-1}=A ( A − 1 ) − 1 = A
若A A A k A kA k A ( k A ) − 1 = 1 k A − 1 (kA)^{-1}=\frac{1}{k}A^{-1} ( k A ) − 1 = k 1 A − 1 k k k
若同阶方阵A . B A.B A . B A B AB A B ( A B ) − 1 = B − 1 A − 1 (AB)^{-1}=B^{-1}A^{-1} ( A B ) − 1 = B − 1 A − 1 例题
矩阵的初等变换
初等变换i , j i,j i , j r i ⟷ r j r_i\longleftrightarrow r_j r i ⟷ r j k ≠ 0 k \ne 0 k = 0 r i × r j r_i \times r_j r i × r j k k k
定义1:行的阶梯型矩阵阶梯型矩阵 A A A A A A r ( A ) 、 R ( A ) r(A)、R(A) r ( A ) 、 R ( A )
用初等变换求矩阵的逆 ( A ∣ E ) > 初等行变换 > ( E ∣ A − 1 ) (A|E)>初等行变换>(E|A^{-1}) ( A ∣ E ) > 初 等 行 变 换 > ( E ∣ A − 1 ) 例题
向量空间 向量及其组合
定义1n n n a 1 , a 2 , … , a n a_1,a_2,…,a_n a 1 , a 2 , … , a n n n n n n n n n n i i i a a a i i i
定义2A : a 1 , a 2 , … , a m A:a_1,a_2,…,a_m A : a 1 , a 2 , … , a m k 1 , k 2 , … , k m k_1,k_2,…,k_m k 1 , k 2 , … , k m k 1 a 1 + k 2 a 2 + … + k m a m k_1a_1+k_2a_2+…+k_ma_m k 1 a 1 + k 2 a 2 + … + k m a m 向量组A A A ,k 1 , k 2 , … , k m k_1,k_2,…,k_m k 1 , k 2 , … , k m
定义3A : a 1 , a 2 , … , a m 、 B : b 1 , b 2 , … , b m A:a_1,a_2,…,a_m、B:b_1,b_2,…,b_m A : a 1 , a 2 , … , a m 、 B : b 1 , b 2 , … , b m B B B A A A 向量组B B B A A A ,若向量组A A A B B B 等价 ;
向量的线性相关与无关性
定义A A A m m m 不全为0 的数k 1 , k 2 , k 3 , … , k m k_1,k_2,k_3,…,k_m k 1 , k 2 , k 3 , … , k m k 1 a 1 + k 2 a 2 + … + k m a m = 0 k_1a_1+k_2a_2+…+k_ma_m=0 k 1 a 1 + k 2 a 2 + … + k m a m = 0 A A A A A A a 1 , a 2 . . . a m a_1,a_2...a_m a 1 , a 2 . . . a m k 1 = k 2 = . . . = k m k_1=k_2=...=k_m k 1 = k 2 = . . . = k m
相关性判定定理A : a 1 , a 2 . . . a m A:a_1,a_2...a_m A : a 1 , a 2 . . . a m ⟺ R ( A ) < m \Longleftrightarrow R(A)<m ⟺ R ( A ) < m m m m ⟺ \Longleftrightarrow ⟺ ⟺ \Longleftrightarrow ⟺ A A A n n n ∣ A ∣ = 0 |A|=0 ∣ A ∣ = 0 A : a 1 , a 2 . . . a m A:a_1,a_2...a_m A : a 1 , a 2 . . . a m ⟺ R ( A ) = m \Longleftrightarrow R(A)=m ⟺ R ( A ) = m m m m ⟺ \Longleftrightarrow ⟺ ⟺ \Longleftrightarrow ⟺ A A A ∣ A ∣ ≠ 0 |A|\ne 0 ∣ A ∣ = 0
其他定理A : a 1 . . . a m ( m ≥ 2 ) A:a_1...a_m(m \ge 2) A : a 1 . . . a m ( m ≥ 2 ) 其中至少有一个向量可由其余m − 1 m-1 m − 1 。α \alpha α β \beta β β \beta β α \alpha α A : a 1 . . . a m A:a_1...a_m A : a 1 . . . a m A 2 : a 1 . . . a m . . . a m + n A_2:a_1...a_m...a_{m+n} A 2 : a 1 . . . a m . . . a m + n 部分相关,整体必定相关 ;α i = ( a i 1 , . . . , a i r ) , ( i = 1 , 2... m ) , β i = ( a i 1 , . . . , a i r , a i , r + 1 ) , ( i = 1 , 2... m ) \alpha _i=(a_{i1},...,a_{ir}),(i=1,2...m),\beta _i=(a_{i1},...,a_{ir},a_{i,r+1}),(i=1,2...m) α i = ( a i 1 , . . . , a i r ) , ( i = 1 , 2 . . . m ) , β i = ( a i 1 , . . . , a i r , a i , r + 1 ) , ( i = 1 , 2 . . . m ) α 1 , . . . , α m \alpha _1,...,\alpha _m α 1 , . . . , α m β 1 , . . . , β m \beta _1,...,\beta _m β 1 , . . . , β m
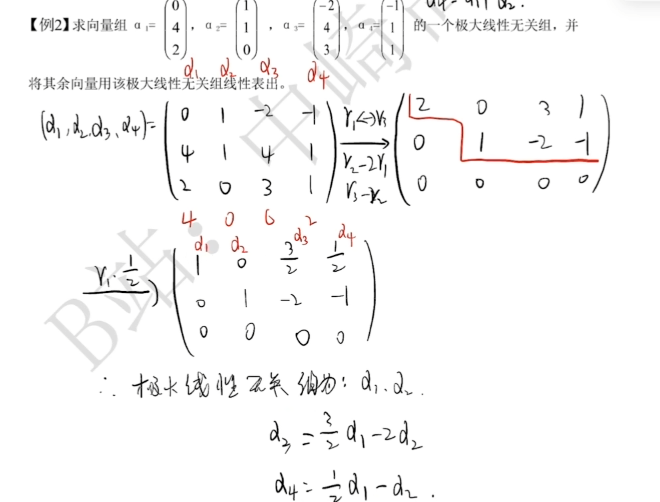
向量的极大线性无关组 例题
线性方程组
概念线性方程组 b 1 , . . . , b m = 0 b_1,...,b_m=0 b 1 , . . . , b m = 0 齐次线性方程组 ;b 1 , . . . , b m b_1,...,b_m b 1 , . . . , b m 非齐次线性方程组 ;
线性方程组矩阵m × n m \times n m × n 常数项(b 1 . . . b m b_1...b_m b 1 . . . b m 构成的m × ( n + 1 ) m \times (n+1) m × ( n + 1 ) 增广矩阵 ,用A ‾ \overline{A} A A = [ a 11 a 12 . . . a 1 n a 21 a 22 . . . a 2 n : : : a m 1 a m 2 . . . a m n ] , X = [ x 1 x 2 : x n ] , b = [ b 1 b 2 : b m ] A=\begin{bmatrix}a_{11}&a_{12}&...&a_{1n}\\a_{21}&a_{22}& ...&a_{2n}\\: &: &&: \\a_{m1}&a_{m2}&...&a_{mn}\end{bmatrix},X=\begin{bmatrix}x_1\\x_2\\: \\x_n\end{bmatrix},b=\begin{bmatrix}b_1\\b_2\\: \\b_m\end{bmatrix} A = ⎣ ⎢ ⎢ ⎢ ⎡ a 1 1 a 2 1 : a m 1 a 1 2 a 2 2 : a m 2 . . . . . . . . . a 1 n a 2 n : a m n ⎦ ⎥ ⎥ ⎥ ⎤ , X = ⎣ ⎢ ⎢ ⎢ ⎡ x 1 x 2 : x n ⎦ ⎥ ⎥ ⎥ ⎤ , b = ⎣ ⎢ ⎢ ⎢ ⎡ b 1 b 2 : b m ⎦ ⎥ ⎥ ⎥ ⎤ A X = b AX=b A X = b A X = 0 AX=0 A X = 0
齐次线性方程组ξ 1 , . . . , ξ s \xi _1,...,\xi _s ξ 1 , . . . , ξ s ξ 1 , ξ 2 . . . ξ s \xi _1,\xi _2...\xi _s ξ 1 , ξ 2 . . . ξ s ξ 1 , . . . , ξ s \xi _1,...,\xi _s ξ 1 , . . . , ξ s ξ 1 , . . . , ξ s \xi _1,...,\xi _s ξ 1 , . . . , ξ s k 1 ξ 1 + . . . + k s ξ s k_1 \xi _1+...+k_s \xi _s k 1 ξ 1 + . . . + k s ξ s A A A R ( A ) = r < n R(A)=r<n R ( A ) = r < n n − r n-r n − r r ( A ) = n r(A)=n r ( A ) = n A X = 0 AX=0 A X = 0 ⟺ \Longleftrightarrow ⟺ ⟺ 为方阵 \Longleftrightarrow 为方阵 ⟺ 为 方 阵 ∣ A ∣ ≠ 0 |A| \ne 0 ∣ A ∣ = 0 r ( A ) < n r(A)<n r ( A ) < n A X = 0 AX=0 A X = 0 ⟺ \Longleftrightarrow ⟺ ⟺ 为方阵 \Longleftrightarrow 为方阵 ⟺ 为 方 阵 ∣ A ∣ = 0 |A| = 0 ∣ A ∣ = 0 n n n
非齐次线性方程组r ( A ) = r ( A ‾ ) = n r(A)=r(\overline{A} )=n r ( A ) = r ( A ) = n r ( A ) = r ( A ‾ ) = r < n r(A)=r(\overline{A})=r<n r ( A ) = r ( A ) = r < n r ( A ) ≠ r ( A ‾ ) r(A)\ne r(\overline{A}) r ( A ) = r ( A ) 当增广矩阵的秩与系数矩阵的秩相等时,非齐次线性方程组才有解; A X = 0 AX=0 A X = 0 A X = B AX=B A X = B X = η 1 X=\eta _1 X = η 1 X = η 2 X= \eta _2 X = η 2 A X = b AX=b A X = b X = η 1 − η 2 X=\eta _1 - \eta _2 X = η 1 − η 2 A X = 0 AX=0 A X = 0 ξ \xi ξ A X = 0 AX=0 A X = 0 ξ ∗ \xi ^* ξ ∗ A X = b AX=b A X = b η = ξ + ξ ∗ \eta = \xi + \xi ^* η = ξ + ξ ∗ A X = b AX=b A X = b η ∗ \eta ^* η ∗ n n n ξ 1 , . . . , ξ n − r \xi _1,...,\xi _{n-r} ξ 1 , . . . , ξ n − r η = η ∗ + k 1 ξ 1 + . . . + k n − r ξ n − r \eta = \eta ^*+k_1\xi _1+...+k_{n-r}\xi _{n-r} η = η ∗ + k 1 ξ 1 + . . . + k n − r ξ n − r 非线性齐次方程组的通解可以简记为:非齐通=齐通+非齐特