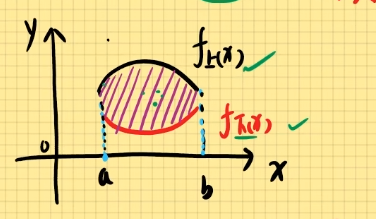多元函数微分学
由多个变量确定的函数称为多元函数。
多元函数的定义域
某函数z,由两个变量确定时,称z=f(x,y)为二元函数.
其定义域为x,y的取值范围。
二元函数定义域写法(x,y)∣x,y需要满足的条件。
例题1:z=y−x2+1,其定义域为(x,y)∣y−x2+1≤0。
例题2:z=ln(x2+y2−4)+9−xf2−y2,其定义域为(x,y)∣y−x2+1≤0。
解:x2+y2−4>0,9−x2−y2≥0
x2+y2>4,x2+y2≤9
4<x2+y2≤9
例题3:z=ln(1−x2−y2)arcsin2x的定义域为(x,y)∣−21≤x≤21且0<x2+y2<1。
解:分子−1≤2x≤1,即−21≤x≤21。
分母ln(1−x2−y2)=0,即1−x2−y2=1,x2+y2=0。
分母1−x2−y2>0,即x2+y2<1。
即分母定义域0<x2+y2<1。
二元函数对应法则
解法:{换元配凑
例题1:f(x+y,x−y)=x2−y2,求f(x,y)。
解:x2−y2=(x+y)(x−y)
f(x+y,x−y)=(x+y)(x−y)
f(x,y)=x⋅y
二元函数的极限
若点P(x,y)以任意方式趋于点P0(x0,y0)时,函数f(x,y)趋于一个常数A,则称A为f(x,y)的极限,记为lim(x,y)→(x0,y0)f(x,y)或limx→x0,y→y0f(x,y)。
例题1:求limx→0,y→2xsinxy。
解:原式=limx→0,y→2xsinxy
=limx→0,y→2xxy=2。
二元函数偏导数
当y0固定而x在x0处有增量Δx时,称limΔx→0Δxf(x0+Δx,y0)−f(x0,y0)为二元函数对x的偏导数。
反之,称limΔy→0Δyf(x0,y0+Δx)−f(x0,y0)为二元函数对y的偏导数。
- 一阶偏导的写法
设二元函数z=f(x,y)
记为∂x∂z或∂x∂f,Zx或fx(x,y)为对x的偏导。
记为∂y∂z或∂y∂f,Zy或fy(x,y)为对y的偏导。
- 一阶偏导的计算
∂x∂z:指对x求偏导,y固定为一个常数(暂时)
∂y∂z:指对y求偏导,x固定为一个常数(暂时)
例题1:已知z=x2+3xy+y2,求∂y∂z=3x+2y。
解:∂y∂z=3x+2y。
例题2:若z=exy⋅sin2y,求∂y∂z=2exy⋅cos2y+xexy⋅sin2y。
解:∂y∂z=x⋅exy⋅sin2y+exy⋅cos2y⋅2=2exy⋅cos2y+xexy⋅sin2y。
例题3:若z=f(x2+y),求∂x∂z=2xf′(x2+y)。
解:∂x∂z=2xf′(x2+y)。
二元函数的全微分
公式:dz=∂x∂zdx+∂y∂zdy。
例题1:设z=x2+xy,求其在(1,0)处的全微分。
解:∂x∂z=2x+y∣(1,0)=2
∂y∂z=x∣(1,0)=1。
dz=∂x∂zdx+∂y∂zdy=2dx+dy。
例题2:设z=f(x2−y2),求其在f处可微,求dz。
解:∂x∂z=f′(x2−y2)⋅2x=2xf′(x2−y2)。
∂y∂z=f′(x2−y2)⋅(−2y)=−2yf′(x2−y2)。
dz=∂x∂zdx+∂y∂zdy=2xf′(x2−y2)dx−2yf′(x2−y2)dy。
例题3:设z=exy2,求dz
解:∂x∂z=exy2⋅y2
∂y∂z=exy2⋅2xy。
dz=exy2⋅y2dx+exy2⋅2xydy。
可微与偏导的关系
可微⟺可导⟹连续⟹极限
z=f(x,y)偏导数存在且连续⟹f(x,y)可微
z=f(x,y)可微⟹连续⟹极限
z=f(x,y)可微⟹偏导存在
偏导存在,与连续无关
例题1:若函数z=f(x,y)在点(x0,y0)某一邻域内偏导∂x∂z,∂y∂z都存在,则z=f(x,y)在(x0,y0)可微。(×)
解析:偏导未连续,不可微。
可微的本质
可微:指用f(x)在(x0,y0)处的切线上的增量Δy来替代了曲线f(x)本身的增量Δy。
{tanθ=ΔxΔyf′(x0)=tanθ⟹f′(x0)=ΔxΔy
⟹Δy切=f′(x0)Δx。
若Δy切=Δy则称可微!
条件:Δy−Δy切=Δy−f′(x0)⋅Δx⟹趋于0且为Δx的高阶无穷小量
具体判断方法:
(1). 写增量:Δy=f(x0+Δx)−f(x0)
(2). 写线性增量:AΔx=f′(x0)⋅Δx
(3). 作极限:limΔx→0ΔxΔy−AΔx=0
(4). 判断:若极限为0,则可微。
在二元函数内:z=f(x,y)
(1). 全增量:Δz=f(x0+Δx,y0+Δy)−f(x0,y0)
(2). 线性增量:Δz=AΔx+BΔy
(3). 作极限:limΔx2+Δy2Δz−Δz线=0
(4). 判断:若极限为0,则可微。
Δz=AΔx+BΔy+0(ρ),ρ=Δx2+Δy2,A=∂x∂z,B=∂y∂z
例题1:设f(x,y)在点(x0,y0)处两个偏导fx(x0,y0),fy(x0,y0)都存在,则有()
A. 存在常数k使得limx→x0,y→y0f(x,y)=k(极限存在)
B. limx→x0,y→y0f(x,y)=f(x0,y0)(连续)
C. limy→y0f(x,y)=f(x0,y0);limx→x0f(x,y)=f(x0,y0)
D. 当(Δx)2+(Δy)2→0时,f(x0+Δx,y0+Δy)−f(x0,y0)−[fx(x0,y0)Δx+fy(x0,y0)Δy]=0((Δx)2+(Δy)2)
解析:偏导存在,没有提连续,不能判断极限存在,AB错,fx(x0,y0)=dxdf(x0,y0)∣x=x0,fy(x0,y0)=dydf(x0,y0)∣y=y0可判断x方向和y方向均为连续,故C正确,偏导+连续才为可微,题目未提连续,即D错误。
二阶偏导
z=f(x,y)的二阶偏导数:
∂x2∂2z指z对x求两次偏导
∂y2∂2z指z对y求两次偏导
∂y∂x∂2z指z先对y后对x的二阶混合偏导
∂x∂y∂2z指z先对x后对y的二阶混合偏导
z=f(x,y)的两个混合偏导
∂x∂y∂2z,∂y∂x∂2z在闭区间D内连续,则
∂x∂y∂2z=∂y∂x∂2z
例题1:设z=x3y2,求∂x2∂2z,∂x∂y∂2z,∂y∂x∂2z。
解:∂x∂z=3x2y2
则∂x2∂2z=6xy2,∂x∂y∂2z=6x2y
∂y∂z=2x3y
∂y∂x∂2z=6x2y
例题2:设z=yx,则zxy=∂x∂y∂2z=()
解:∂x∂z=yx⋅lny
∂x∂y∂2z=(yx)′⋅lny+yx⋅(lny)′=x⋅yx−1lny+yx⋅x1
=yx−1(xlny+1)
二元隐函数求一阶偏导
不是z=f(x,y)的二元函数,叫隐函数。
用公式法求二元隐函数的一阶偏导
(1). 令F(x,y,z)
(2). 求Fx,Fy,Fz
(3). 套公式:∂x∂z=−FzFx,∂y∂z=−FzFy
例题1:设z=z(x,y)由方程z+ez=xy所确定,求∂x∂z,∂y∂z。
解:令F(x,y,z)=z+ez−xy
Fx=−y,Fy=−x,Fz=1+ez
∂x∂z=−FzFx=1+ezy,∂y∂z=−FzFy=1+ezx
例题2:由方程xyz+x2+y2+z2=2所确定的函数z=z(x,y)在点(1,0,-1)处的全微分dz=。
解析:全微分:dz=∂x∂zdx+∂y∂zdy
解:令F(x,y,z)=xyz+x2+y2+z2−2
Fx=yz+2x2+y2+z21⋅2x∣(1,0,−1)=21=22
Fx=xz+2x2+y2+z21⋅2y∣(1,0,−1)=−1
Fx=xy+2x2+y2+z21⋅2z∣(1,0,−1)=−21=−22
∂x∂z=−FzFx=−−2222=1
∂y∂z=−FzFy=−22−1=−2
dz=∂x∂zdx+∂y∂zdy
=dx−2dy
隐函数的二阶偏导
(1). 使用公式求一阶导;
(2). 使用导数公式求二阶导;
注:求二阶导时,切记z是关于x,y的函数需要求导的。
例题1:设2x2+y2+z2−4z=0其中z=z(x,y)所确定,求∂x∂z∣(1,1,1),∂x2∂2z∣(1,1,1)。
解:令F(x,y,z)=2x2+y2+z2
则Fx=4x∣(1,1,1)=4,Fy=2y∣(1,1,1)=2,Fz=2z−4∣(1,1,1)=−2
故∂x∂z=−FzFx=2e−4−4x∣(1,1,1)=2
∂x2∂2z=∂x∂(∂x∂z)=(z−2)22⋅(z−2)+2x⋅(∂x∂z)∣(1,1,1)=6
多元复合函数求导
求导原则:从外向里,层层求导并相乘。
链式法则:将每层函数关系罗列(树状图)分线相加,连线相乘

- 题型一:具体多元函数求导(直接带入法)
例题1:设z=xy+3lnx,其中x=2u+v,y=u−2v,求∂u∂z,∂v∂z。
解:由题可知:z=(2u+v)⋅(u−2v)+3ln(2u+v) ∂u∂z=2(u−2v)+(2u+v)+3⋅2u+v1⋅2=4u−3v+2u+v6
∂v∂z=(u−2v)+(2u+v)⋅(−2)+3⋅2u+v1=−3u−4v+2u+v1
- 题型二:抽象的复合函数求导
面对含f(□,△)的复合求导。
注:(1). 从外向里,逐层求导;
(2). 勿忘f要导f’;
(3). “□“用“1”代替,”△“用“2”代替。
(4). 计算结果内容省略不写括号;
例题1:设z=f(x,xy),求∂x∂z,∂y∂z。
解:∂x∂z=f1′x,xy⋅1+f2′(x,xy)⋅y=f1′+y⋅f2′ ∂y∂z=f2′(x,xy)⋅x=x⋅f2′
例题2:设z=xyf(x+y,x−y2),其中f可微,求∂x∂z,∂y∂z。
解:∂x∂z=yf+xy⋅[f1′⋅2x+f2′⋅1]=yf+2x2yf1′+xyf2′ ∂y∂z=xf+xy[f1′⋅1−f2′⋅2y]=xf+xyf1′−2xy2f2′
例题3:设z=f(xy,y),其中f具有二阶连续偏导,求∂x∂y∂2z。
解:∂x∂z=f1′(xy,y)⋅y=yf1′(xy,y) ∂x∂y∂2z=f1′⋅1+y[f11′′⋅x+f12′′⋅1
=f1′+xyf1′′+f11′′+yf12′′
隐函数例题
例题1:设函数u=f(x,y,z)=x3y2z2,其中z=z(x,y)由方程x3+y3+z3−3xyz=0所确定,求∂x∂u。
解:∂x∂u=3x2y2z2+x3y2⋅2z⋅∂x∂z
令F(x,y,z)=x3+y3+z3−3xyz
Fx=3x2−3yz,Fz=3z2−3xy
∂x∂z=−FzFx=−3z2−3xy3x2−3yz=z2−xyyz−x2
∂x∂u=3x2y2z2+2x3y2z⋅(z2−xyyz−x2)
多元函数的几何的应用
- 求空间曲线⎩⎪⎨⎪⎧x=x(t)y=y(t)z=z(t)的切线及法平面方程。 {直线:mx−x0=ny−y0=pz−z0,S=(m,n,p)平面:A(x−x0)+B(y−y0)+C(z−z0)=0,n=(A,B,B)
解法:
(1). 求导得向量:S=(x′(t),y′(t),z′(t))=(m,n,p)/n=(x′(t),y′(t),z′(t))=(A,B,C)
(2). 套公式得答案:“线除面乘”。 {线:x′(t)x−x0=y′(t)y−y0=z′(t)z−z0面:x′(t)(x−x0)+y′(t)(y−y0)+z′(t)(z−z0)
例题1:求螺旋线x=acosθ,y=asinθ,z=bθ(a,b不同时为0),上在θ=4π时的切线方程及法平面方程。
解:令θ=t,则⎩⎪⎨⎪⎧x=acosty=asintz=bt
即x′(t)=−asint,y′(t)=acost,z′(t)=b
当θ=t=4π
则有x′(t)=−22a,y′(t)=22a,z′(t)=b (x0,y0,z0)=(−22a,22a,4bπ)
故切线S=(−22a,22a,b)
法平面n=(−22a,22a,b)
即切线方程−22ax−22a=22ay−22a=bz−4πb
法平面为−22a(x+22a)+22a(y−22a)+b(−4πb)=0
例题2:求曲线y=sinx,z=2x在点(π,0,2π)的法平面方程。
解析:若不是参数方程,令其中一个变量为t,转换为参数式;
解:令x=t,则y=sint,z=2t x′(t)=1,y′(t)=cost,z′(t)=21
因为在点(π,0,2π)处,则x0=t=π x′(t)=1,y′(t)=−1,z′(t)=21
n=(1,−1,21)
(x0,y0,z0)=(π,0,2π)
带入解得法平面方程:1⋅(x−π)−1⋅(y−0)+21⋅(z−2π)=0 x−y+2z−45π=0
例题3:求曲线l:x=t,y=t2,z=t3上的一点,使得曲线在该点处的切线平行于平面3x+3y+z=0。
解析:线与面位置关系与向量关系相反,由题,线与面平行,即线与法线垂直,即S⊥n=S⋅n=0
解:令曲线待求点(t0,t02,t03)
故在该点处S=(1,2t0,3t03)
有平面方程得n=(3,3,1)
由题知:S⋅n=0 3+6t0+3t02=0
解得t0=−1
故点为(−1,1,−1)
- 空间曲面F(x,y,z)的切平面和法线方程。
解法:
(1). 求导得向量:n=(A,B,C)=(Fx,Fy,Fz)/S=(m,n,p)=(Fx,Fy,Fz)
(2). 套公式得答案:“线除面乘”。 {线:x′(t)x−x0=y′(t)y−y0=z′(t)z−z0面:x′(t)(x−x0)+y′(t)(y−y0)+z′(t)(z−z0)
例题1:空间曲面2z−ez+2xy=3在点(1,2,0)处的法线方程。
解:令F(x,y,z)=2z−ez+2xy−3 S=(Fx,Fy,Fz)=(2y,2x,2−ez)∣(1,2,0)=(4,2,1)
故法线方程:4x−1=2y−2=1z
例题2:已知曲面z=4−x2−y2在点P处的切平面平行于平面2x+2y+z−1=0,求P点坐标。
解:设P点为(x0,y0,z0),令F(x,y,z)=z−4+x2+y2
所以在P点处切平面n1=(Fx,Fy,Fz)=(2x,2y,1)∣(x0,y0,z0)=(2x0,2y0,1)
又平面2x+2y+z−1=0的法向量为n2=(2,2,1)
由题知:n1∥n2
即22x0=22y0=1
解得x0=y0=1
带入得z0=2
故点为P=(1,1,2)
无条件极值
无条件极值:指对x,y取值范围无限制下,求z=f(x,y)的极值。
求解方法:
(1). 求一阶偏导,令其为0,找驻点;
{fx(x,y)=0fy(x,y)=0⟹驻点(x0,y0)
(2). 解方程组,求出极值点;
令A=fxx(x0,y0);B=fxy(x0,y0);C=fyy(x0,y0)
(3). 判断AC−B2=D。
D>0,有极值⟹{A<0,极大值A>0,极小值
例题1:求函数f(x,y)=x2−xy+y2−2x+y的极值。
解:令{fx=2x−y−2=0fy=−x+2y+1=0⟹驻点(1,0)
A=fxx=2,B=fxy=−1,C=fyy=2
D=AC−B2=4−1=3>0
且A=2>0
故f(1,0)处为极小值-1。
例题2:求函数f(x,y)=x3−4x2+2xy−y2的极值。
解:令{fx=3x2−8x+2y=0fy=2x−2y=0⟹驻点(0,0),(2,2)
A=fxx=6x−8,B=fxy=2,C=fyy=−2
(1). 当驻点为(0,0)时,A=−8,B=2,C=−2
D=AC−B2=16−4=12>0
且A=−8<0
故f(0,0)处有极大值0。
(2). 当驻点为(2,2)时,A=4,B=2,C=−2
D=AC−B2=−8−4=−12<0
故f(2,2)处没有极值。
条件极值
条件极值:指对自变量x,y取值范围限制下,求z=f(x,y)的极值。
求在条件φ(x,y)=0下,求z=f(x,y)的极值。
解法:
(1). 确定目标函数f(x,y),及条件函数φ(x,y);
(2). 构造拉格朗日函数;F(x,y,λ)=f(x,y)+λφ(x,y)
(3). 令⎩⎪⎨⎪⎧Fx=0Fy=0Fλ=0⟹得驻点(x0,y0)
(4). 得极值。
例题:求函数z=x2+y2在直线4x+3y=1下的极值。
解:目标函数f(x,y)=x2+y2,条件函数φ(x,y)=4x+3y−1=0
令F(x,y,λ)=x2+y2+λ(4x+3y−1)
Fx=2x+4λ=0,Fy=2y+3λ=0,Fλ=4x+3y−1=0
解得x0=−2536,y0=−2548⟹(2536,2548)为唯一驻点
故z=x2+y2在(2536,2548处取得极值
z=(2536)2+(2548)2=25144
条件极值例题
例题1:在椭圆x2+4y2=4上求一点,使其到直线2x+3y−6=0的距离最短。
解:设点为(x0,y0),则点到直线的距离为d=22+32∣2x0+3y0−6∣=13∣2x0+3y0−6∣
令目标函数为2x+3y−6,条件函数为x2+4y2−4=0
令拉格朗日函数为F(x,y,λ)=2x+3y−6+λ(x2+4y2−4)
Fx=2+2λx=0,Fy=3+8λy=0,Fλ=x2+4y2−4=0
解得x0=±58,y0=±53
故点为(58,53),(−58,−53)为驻点
(1). 当(x0,y0)=(58,53)时
带入=13∣2x+3y−6∣=13∣516+59−6∣=13∣5−6∣=1313
(2). 当(x0,y0)=(−58,−53)时
带入=13∣2x+3y−6∣=13∣−516−59−6∣=13∣−5−6∣=131113
故点为P(58,53)时,到直线距离最短,最短距离为1313。
二重积分
二重积分概念与性质
- 定义:二重积分是用来求解曲顶柱体体积的工具,记为∬f(x,y)dx,dy。
其中f(x,y)为被积函数(求图形体积的h),dxdy=dδ面积元素,D为积分区域(底面积)。 V=D∬f(x,y)dxdy
- 性质:
(1). D∬f(x,y)±g(x,y)dxdy=D∬f(x,y)dxdy±g(x,y)dxdy
(2). 可加性D=D1+D2,D∬f(x,y)dxdy=D1∬f(x,y)dxdy+D2∬f(x,y)dxdy
(3). D∬kf(x,y)dxdy=kD∬f(x,y)dxdy
(4). 底面积计算公式:D∬1⋅dxdy=D∬dxdy=SD
(5). 比较定理:设f(x,y)≥g(x,y),则D∬f(x,y)dxdy≥D∬g(x,y)dxdy反比f(x,y)的大小
(6). 估值定理:设f(x,y)在D上,有最大值M和最小值m,有m≤f(x,y)≤M
则有⟹D∬mdxdy≤D∬f(x,y)dxdy≤D∬Mdxdy⟹mD∬dxdy≤D∬f(x,y)dxdy≤MD∬dxdy⟹m⋅SD≤D∬f(x,y)dxdy≤M⋅SD
二重积分性质考点计算
D∬1⋅dxdy=SD
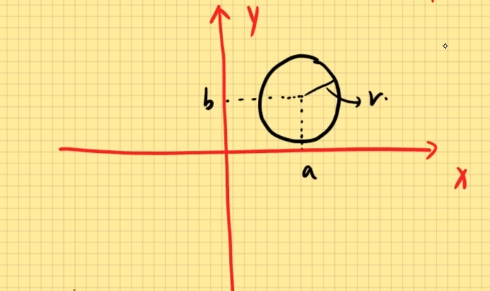
(1). 圆的一般表达式:(x−a)2+(y−b)2=r2
其中,(a,b)为圆心,r为半径。
S圆=π⋅r2

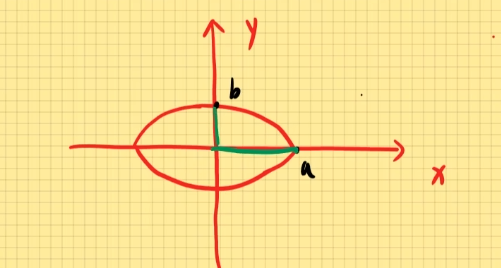
(2). 椭圆的一般表达式:a2x2+b2y2=1

S椭圆=π⋅a⋅b
例题1:计算D∬dδ其中D为原点为圆心,半径为5的圆形区域。
解:D∬dδ=SD=π⋅52=25π
例题2:计算二重积分x2+y2≤2∬dxdy
解:由题知:x2+y2≤2取x2+y2=2
因为x2+y2=2为圆的一般表达式,SD=π⋅r2<2时在圆面积内部
x2+y2≥2∬dxdy=SD=π⋅r2=2π。
例题3:设积分区域D:1≤x2+y2≤4求二重积分D∬dxdy
解:由题知:1≤x2+y2≤4取x2+y2=1,x2+y2=4
则D∬dx=SD=SD大−SD小=4π−π=3π
例题4:设积分区域D:4x2+y2≤1求二重积分D∬xdxdy
解:由题知:4x2+y2≤1取4x2+1y2=1
因为4x2+1y2=1为椭圆的一般表达式,SD=π⋅a⋅b<1时在椭圆面积内部
D∬xdxdy=SD=π⋅a⋅b=π⋅2⋅1=2π。
二重积分性质考点比较
(1). 比较定理:设f(x,y)≥g(x,y),则D∬f(x,y)dxdy≥D∬g(x,y)dxdy
例题1:设I1=D∬cosx2+y2dxdy,I2=D∬cos(x2+y2)dxdy,I3=D∬cos(x2+y2)2dxdy其中D={(x,y)∣x2+y2≤1}则I1,I2,I3的大小关系是。
解:x2+y2≤1时比较
取一特殊值x2+y2=41得x2+y2≥x2+y2≥(x2+y2)2
当x2+y2≤1时,1≥x2+y2≥x2+y2≥(x2+y2)2≥0

由图I3≥I2≥I1
二重积分性质考点估值
估值定理:设f(x,y)在D上,有最大值M和最小值m,有m≤f(x,y)≤M,则m⋅SD≤D∬f(x,y)dxdy≤M⋅SD
例题1:设I=D∬xy(x+y)dxdy其中0≤x≤1,0≤y≤2则()≤I≤()。
解:

由图知:SD=1⋅2=2
因为0≤x≤1,0≤y≤2
则x=0,y=0时为最小值,x=1,y=2时为最大值
即0≤xy(x+y)≤6
0⋅SD≤D∬xy(x+y)dxdy≤6⋅SD
0≤D∬xy(x+y)dxdy≤6⋅2
0≤D∬xy(x+y)dxdy≤12
二重积分的计算
- 直角坐标系下二重积分计算
解法:将二重积分化为累次积分或二次积分。
(1). D∬f(x,y)dxdy=∫abdx∫cdf(x,y)dy
(1). D∬f(x,y)dxdy=∫cddy∫abf(x,y)dx
注:求解顺序,先求尾部再求前面,从后往前,从右到左依次求解
根据积分区域图形不同,选择不同积分顺序。
1). X型图:函数图形,由上下两函数,夹为一个图形;

公式:D∬f(x,y)dxdy=∫abdx∫f上(x)f下(x)f(x,y)dy
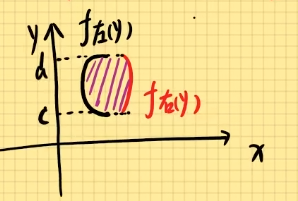
2). Y型图:函数图形,由左右两函数,合为一个图形:改函数f(y);

公式:D∬f(x,y)dxdy=∫cddy∫f左(y)f右(y)f(x,y)dx
定限口诀:后积先定限,限内画直线,先交写下限,后交写上限。
- 二重积分直角坐标系下计算例题
求解过程:
(1). 画图,联立方程,求出曲线交点。
(2). 判断积分区域类型,确定积分顺序。
(3). 套公式{X⟹∫□□dx∫□□f(x,y)dyY⟹∫□□dy∫□□f(x,y)dx。
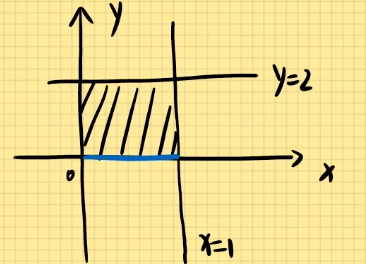
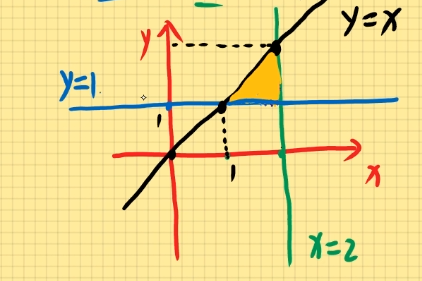
例题1:计算二重积分D∬xydxdy其中D为由直线y=1,x=2,y=x围成的区域。
解:

定为X型图:{1≤x≤21≤y≤x
原式=∫12dx∫1xxydy =∫12(x⋅21y2)∣1xdx
=21∫12(x3−x)dx
=21⋅(41x4−21x2)∣21
=89
定为Y型图:{1≤y≤2y≤x≤2
原式=∫12dy∫y2xydx =21∫12y⋅x2∣y2dy
=21∫12(4y−y3)dy
=21⋅(2y2−41y4)∣21
=89
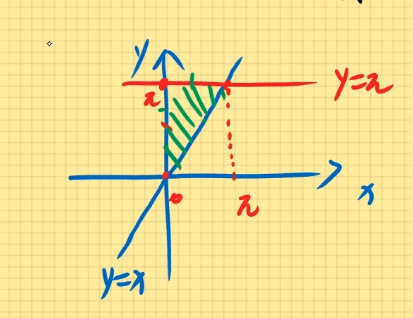
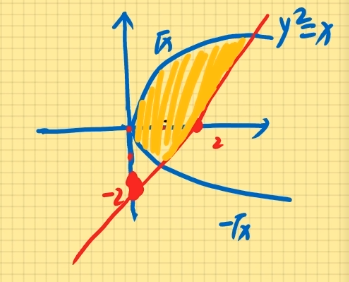
例题2:计算二重积分D∬xydxdy其中D为由直线y2=x,y=x−2围成的区域。
解:

联立两个方程:y2=x,y=x−2
求得两个交点为(−1,1),(4,2)
定为Y型图:{−1≤y≤2y2≤x≤y+2
原式=∫−12dy∫y2y+2xydx =21∫−12y⋅x2∣y2y+2dy
=21∫−12(y3+4y2+4y−y5)dy
=21⋅(41y4+34y3+2y2−61y6)∣2−1
=845
超越积分顺序选择
(1). xsinx,xcosx,sinx2⋅cosx2,ex2,e−x2⟹X型
(2). ysiny,ycosy,siny2⋅cosy2,ey2,e−y2⟹Y型
例题1:求二重积分D∬ysinydxdy其中D为由直线y=x,x=0,y=π围成的区域。
解:

定为Y型图:{0≤y≤π0≤x≤y
原式=∫0πdy∫0yysinydx
=∫0πysiny⋅x∣y0dy
=∫xπsinydy=(−cosy)∣π0=1+1=2
例题2:求二重积分D∬cosy2dxdy其中D为由直线y=2,x=1,y=x−1围成的区域。
解:

定为Y型图:{0≤y≤21≤x≤y+1
故原式=∫02dy∫1y+1cosy2dx
=∫02cosy2⋅x∣y+11dy
=∫02[cosy2(y+1)−cosy2]dy
=21∫02cosy2ydy2
=21siny2∣20=2sin4
交换积分次序
定义:将X型与Y型积分顺序互换;
交换次序思路:
(1). 根据积分上下限,画出积分区域
(2). 交换次序
交换次序的题型:
(1). 题目要求交换
(2). 遇积分上下限定好的二重积分计算
例题1:二次积分∫01dx∫2x2xf(x,y)dy交换积分次序。
A. ∫01dx∫2yyf(x,y)dy
B. ∫02dy∫4y22yf(x,y)dx
C. ∫2x2xf(x,y)dy∫01dx
D. ∫4y22ydy∫02f(x,y)dx

解:由题可知:0≤x≤1,2x≤y≤2x
有图可知:0≤y≤2,4y2≤x≤2y
故选B。
例题2:求积分I=∫4121dy∫21yexydx+∫211dy∫yyexydx交换积分次序。
解析:∫4121dy∫21yexydx可知
{41≤y≤2121≤x≤y
∫211dy∫yyexydx可知
{21≤y≤1y≤x≤y

选择X型:{21≤x≤1x2≤y≤x
原式∫121dx∫x2xexydy
∫121x⋅exy∣xx2dx
∫121x⋅(e−ex)dx
∫121xe−xexdx
e∫121xdx−∫211xexdx
e21x2∣121−∫211xdex
e21(1−41)−[(xex)∣121−∫211exdx]
83e−[e−21e21−e+e21]
83e−2e
极坐标系下的二重积分
- 极坐标系
极坐标系是在平面直角坐标系的基础上,引入极轴(距离)和极角(角度)的坐标系。
由极心,极轴,极径,极角组成。


由图可知:sinθ=ry⟹y=rsinθ cosθ=rx⟹x=ycosθ
小结:在极坐标下,x=rcosθ,y=rsinθ,x2+y2=r2
- 极坐标系下二重积分计算
(1). 条件:当遇到与圆相关的积分区域(圆,半圆,扇形,弧形……)。
(2). 考虑利用极坐标求解。
常见的函数:xy,x2+y2
(3). 转换:令x=rcosθ,y=rsinθ,dady=rdrdθ
(4). 公式:D∬f(x,y)dxdy=(极)∫θ1θ2dθ∫r1r2f(rcosθ,rsinθ)⋅rdr
- 上下限的确定方法
(1). 夹角θ的取值范围:
从原点出发,逆时针方向作积分区域的两条切线,取第一条触碰积分区域的切线与x正半轴的夹角为θ1。
取第二条触碰积分区域的切线与x正半轴的夹角为θ2。

∫θ1θ2dθ
(2). 半径r的取值范围
OA=r1,OB=r2,则r1,r2为积分区域的内外半径。

r的计算方法:将x=rcosθ,y=rsinθ,x2+y2=r2代入积分区域的方程,得到r1,r2的表达式。
注意:0≤r
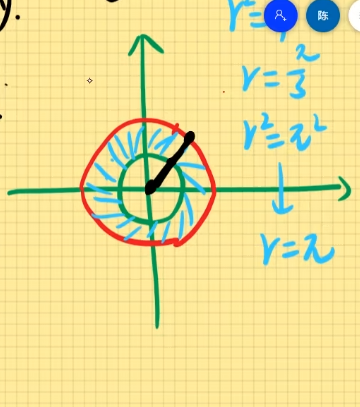
常见积分区域(图像):
(1). 圆
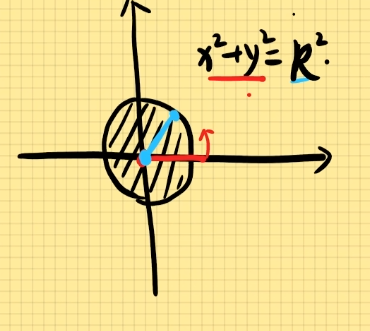
一般式方程:x2+y2=R2,其中R为半径,(a,b)为圆心。

其中:0≤θ≤2π,0≤r≤R
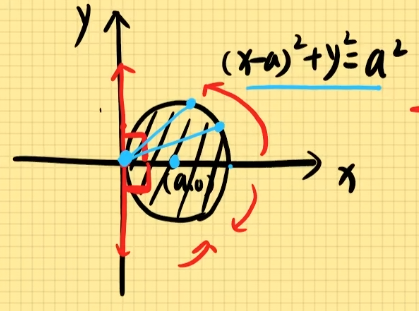
(2). 偏离原点,圆心在x轴上的圆形

(x−a)2+y2=a2,其中a为半径,(a,0)为圆心。
由图:−2π≤θ≤2π,0≤r≤2acosθ
展开方程式:x2−2ax+a2+y2=a2
x2+y2=2ax
即r2=2a⋅rcosθ
r=2acosθ
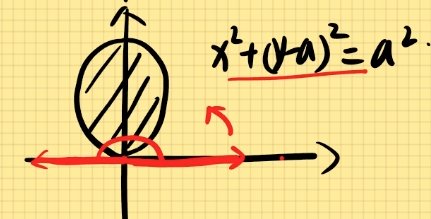
(3). 偏离原点,圆心在y轴上的圆形

x2+(y−b)2=b2,其中b为半径,(0,b)为圆心。
由图:0≤θ≤π,0≤r≤2asinθ
展开方程式:x2+y2−2ay+a2=a2
x2+y2=2ay
即r2=2a⋅rsinθ
r=2asinθ
例题1:设积分区域为:D由x2+y2=9π2,x2+y2=π2围成,求D∬x2+y2sinx2+y2dxdy
解:令x=rcosθ,y=rsinθ,x2+y2=r2

由题可知r1=3π,r2=π
可知:0≤θ≤2π,3π≤r≤π
由原式可得:∫02πdθ∫3ππr2sinr2dxdy
∫02πdθ∫3ππrsinrdr
∫02π(−cosr)∣π 3πdθ
∫02π23dθ
23θ∣2π 0
3π
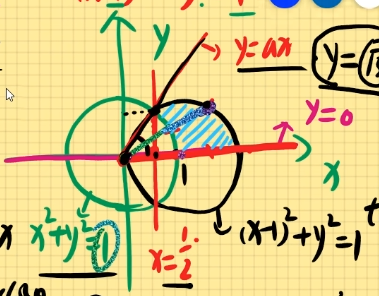
例题2:求二重积分D∬x2+y2dxdy其中D:x2+y2=1,x2+y2=2x,y=0围成的区域在第一象限部分且x≥21。
解:由题可知:x2+y2=2x和x2+y2=1
可得:x2−2x+1−1+y2=0,(x−1)2+y2=1
即圆心为(1,0),r=1和(0,0),r=1

令x=rcosθ,y=rsinθ,x2+y2=r2,dxdy=rdrdθ
过原点作切线y=ax
将x=21带入x2+y2=2x得y=23
将x=21,y=23带入y=ax得a=3
则切线方程为y=3x
则tanθ=3
则θ=3π
因为x2+y2=r2,x2+y2=2x
则有r1=1,r2=2cosθ
即得{0≤θ≤3π1≤r≤2cosθ
则原式=∫03πdθ∫12cosθrrdr
=∫03πdθ∫12cosθ1⋅dr
=∫03π(2cosθ−1)dθ
=2sinθ−θ∣3π0
=3−3π
二重积分的对称性
(1). 条件:f(−x,y)=f(x,y),D∬f(x,y)dxdy=2D1∬f(x,y)dxdy
(2). 条件:f(−x,y)=−f(x,y),D∬f(x,y)dxdy=0
由上条件可以看出:y不变f(−x)=f(x)为偶函数,或f(−x)=−f(x)为奇函数
则二重积分的偶倍奇零。
(1). 积分区域D关于y轴对称,看x的奇偶性;
D∬f(x,y)dxdy=关于x函数{2D1∬f(x,y)dxdy为偶函数0,为奇函数
(2). 积分区域D关于x轴对称,看y的奇偶性;
D∬f(x,y)dxdy=关于y函数{2D1∬f(x,y)dxdy为偶函数0,为奇函数
注意:若D对称,首选对称性
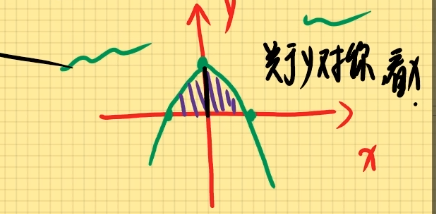
例题1:设D由y=1−x2及x轴围成,则D∬(sinx+x3y)dxdy
A. 34 B. 32 C.1 D. 0
解:

由图可知,函数关于y对称
由题可知:sinx为奇函数,x3y为奇函数,即选D
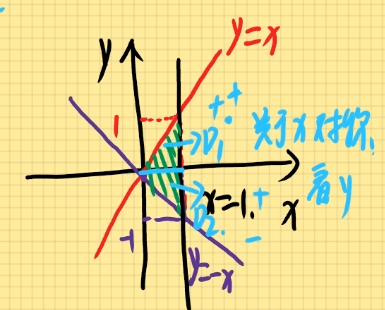
例题2:求I=D∬xy(x+y)dxdy其中D:由y=x,x+y=0,x=1围成
解:

由原式得:D∬x2y+xy2dxdy
由偶倍奇零和对称性得知:D1∬xy2dxdy
2∫01dx∫0xxy2dy
2∫01(x⋅31y3)∣0xdx
2∫0131x4dx
32⋅51x5∣01
32⋅5115=152