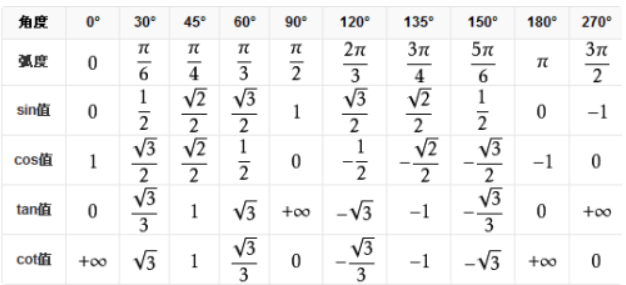
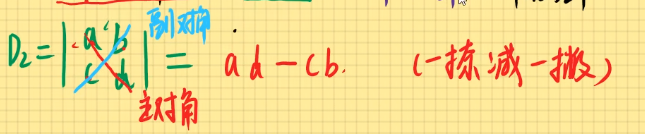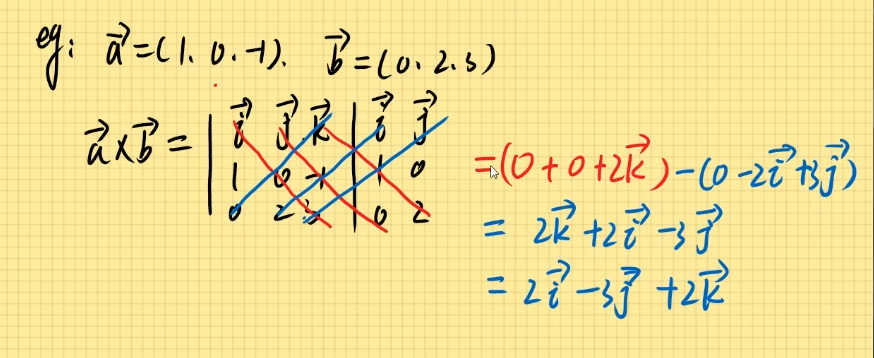向量代数与空间解析几何 向量的概念
向量(矢量)是有大小有方向的量,用一个带箭头的线段来表示,线段的长度表示向量的大小,箭头的方向表示向量的方向a ⃗ \vec{a} a
标量(数量)是只有大小没有方向的量,用一个数字来表示。模来表示,向量的方向用方向角来表示。
向量在坐标系中的表示:A ( x 1 , y 1 , z 1 ) , B ( x 2 , y 2 , z 2 ) A(x_1,y_1,z_1),B(x_2,y_2,z_2) A ( x 1 , y 1 , z 1 ) , B ( x 2 , y 2 , z 2 ) A B ⃗ = ( x 2 − x 1 , y 2 − y 1 , z 2 − z 1 ) \vec{AB}=(x_2-x_1,y_2-y_1,z_2-z_1) A B = ( x 2 − x 1 , y 2 − y 1 , z 2 − z 1 )
向量的大小(模长):∣ A B ⃗ ∣ = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + ( z 2 − z 1 ) 2 |\vec{AB}|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2} ∣ A B ∣ = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + ( z 2 − z 1 ) 2
单位向量:模长为1的向量(e ⃗ \vec{e} e A B ⃗ \vec{AB} A B A B ⃗ ∣ A B ⃗ ∣ \frac{\vec{AB}}{|\vec{AB}|} ∣ A B ∣ A B A B ⃗ \vec{AB} A B − A B ⃗ ∣ A B ⃗ ∣ -\frac{\vec{AB}}{|\vec{AB}|} − ∣ A B ∣ A B
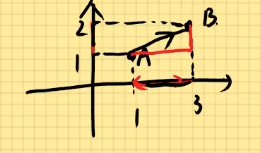
零向量:模长为0的向量(方向任意)。A B ⃗ \vec{AB} A B A B ⃗ \vec{AB} A B A B ⃗ = ( 1 − 1 , 1 − 0 , 4 − 2 ) = ( 0 , 1 , 2 ) \vec{AB}=(1-1,1-0,4-2)=(0,1,2) A B = ( 1 − 1 , 1 − 0 , 4 − 2 ) = ( 0 , 1 , 2 ) ∣ A B ⃗ ∣ = 0 2 + 1 2 + 2 2 = 5 |\vec{AB}|=\sqrt{0^2+1^2+2^2}=\sqrt{5} ∣ A B ∣ = 0 2 + 1 2 + 2 2 = 5 e ⃗ = A B ⃗ ∣ A B ⃗ ∣ = ( 0 , 1 , 2 ) 5 \vec{e}=\frac{\vec{AB}}{|\vec{AB}|}=\frac{(0,1,2)}{\sqrt{5}} e = ∣ A B ∣ A B = 5 ( 0 , 1 , 2 )
基础公式 ∣ a ⃗ + b ⃗ ∣ = ( a ⃗ + b ⃗ ) 2 |\vec{a}+\vec{b}|=\sqrt{(\vec{a}+\vec{b})^2} ∣ a + b ∣ = ( a + b ) 2 ∣ a ⃗ − b ⃗ ∣ = ( a ⃗ − b ⃗ ) 2 |\vec{a}-\vec{b}|=\sqrt{(\vec{a}-\vec{b})^2} ∣ a − b ∣ = ( a − b ) 2 a ⃗ ⋅ b ⃗ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ ⋅ cos < a ⃗ , b ⃗ > \vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}|\cdot \cos <\vec{a},\vec{b}> a ⋅ b = ∣ a ∣ ∣ b ∣ ⋅ cos < a , b > 空间直角坐标系及其单位向量
i ⃗ , j ⃗ , k ⃗ \vec{i},\vec{j},\vec{k} i , j , k 注意:若2 i ⃗ + 3 j ⃗ − 2 k ⃗ 2\vec{i}+3\vec{j}-2\vec{k} 2 i + 3 j − 2 k
向量的运算法则 设a ⃗ = ( x 1 , y 1 , z 1 ) , b ⃗ = ( x 2 , y 2 , z 2 ) \vec{a}=(x_1,y_1,z_1),\vec{b}=(x_2,y_2,z_2) a = ( x 1 , y 1 , z 1 ) , b = ( x 2 , y 2 , z 2 )
向量的加减法: a ⃗ ± b ⃗ = ( x 1 ± x 2 , y 1 ± y 2 , z 1 ± z 2 ) \vec{a}\pm \vec{b}=(x_1\pm x_2,y_1\pm y_2,z_1\pm z_2) a ± b = ( x 1 ± x 2 , y 1 ± y 2 , z 1 ± z 2 )
向量的数乘: k a ⃗ = ( k x 1 , k y 1 , k z 1 ) k\vec{a}=(kx_1,ky_1,kz_1) k a = ( k x 1 , k y 1 , k z 1 )
点乘(数量积): a ⃗ ⋅ b ⃗ = x 1 ⋅ x 2 + y 1 ⋅ y 2 + z 1 ⋅ z 2 \vec{a}\cdot \vec{b}=x_1\cdot x_2+y_1\cdot y_2+z_1\cdot z_2 a ⋅ b = x 1 ⋅ x 2 + y 1 ⋅ y 2 + z 1 ⋅ z 2
叉乘(向量积): a ⃗ × b ⃗ = c ⃗ \vec{a}\times \vec{b}=\vec{c} a × b = c c ⃗ ⊥ a ⃗ c ⃗ ⊥ b ⃗ } c ⃗ = a ⃗ × b ⃗ \left.\begin{matrix}\vec{c} \perp \vec{a} \\\vec{c} \perp \vec{b} \end{matrix}\right\}\vec{c} =\vec{a}\times \vec{b} c ⊥ a c ⊥ b } c = a × b
向量点乘的几何运算 在坐标下:a ⃗ ⋅ b ⃗ = ∣ a ⃗ ∣ ⋅ ∣ b ⃗ ∣ ⋅ c o s θ \vec{a}\cdot \vec{b}=|\vec{a}|\cdot |\vec{b}|\cdot cos\theta a ⋅ b = ∣ a ∣ ⋅ ∣ b ∣ ⋅ c o s θ a ⃗ ⋅ b ⃗ = ∣ a ⃗ ∣ ⋅ ∣ b ⃗ ∣ ⋅ cos θ , θ \vec{a}\cdot \vec{b}=|\vec{a}|\cdot |\vec{b}|\cdot \cos \theta ,\theta a ⋅ b = ∣ a ∣ ⋅ ∣ b ∣ ⋅ cos θ , θ a ⃗ , b ⃗ \vec{a},\vec{b} a , b a ⃗ ⊥ b ⃗ \vec{a}\perp \vec{b} a ⊥ b a ⃗ ⋅ b ⃗ = ∣ a ⃗ ∣ ⋅ ∣ b ⃗ ∣ ⋅ cos 90 ° = 0 \vec{a}\cdot \vec{b} =|\vec{a} |\cdot |\vec{b} |\cdot \cos 90°=0 a ⋅ b = ∣ a ∣ ⋅ ∣ b ∣ ⋅ cos 9 0 ° = 0 a ⃗ ⋅ b ⃗ = 0 ⇔ a ⃗ ⊥ b ⃗ {\color{Red} \vec{a}\cdot \vec{b}=0\Leftrightarrow \vec{a}\perp \vec{b}} a ⋅ b = 0 ⇔ a ⊥ b ( a ⃗ ) 2 = ∣ a ⃗ ∣ × ∣ a ⃗ ∣ ⋅ cos 0 = ∣ a ⃗ ∣ 2 {\color{Red} (\vec{a})^2=|\vec{a}|\times |\vec{a}|\cdot \cos 0=|\vec{a}|^2 } ( a ) 2 = ∣ a ∣ × ∣ a ∣ ⋅ c o s 0 = ∣ a ∣ 2 a ⃗ = ( 2 , λ , − 1 ) , b ⃗ = ( λ , 2 , 5 ) \vec{a}=(2,\lambda ,-1),\vec{b}=(\lambda ,2,5) a = ( 2 , λ , − 1 ) , b = ( λ , 2 , 5 ) λ = 5 4 \lambda =\frac{5}{4} λ = 4 5 a ⃗ ⋅ b ⃗ = 0 \vec{a}\cdot \vec{b}=0 a ⋅ b = 0 2 λ + 2 λ − 5 = 0 2\lambda +2\lambda -5=0 2 λ + 2 λ − 5 = 0 λ = 5 4 \lambda =\frac{5}{4} λ = 4 5 ∣ a ⃗ ∣ = 3 , ∣ b ⃗ ∣ = 2 |\vec{a}|=3,|\vec{b}|=2 ∣ a ∣ = 3 , ∣ b ∣ = 2 a ⃗ ⊥ b ⃗ \vec{a}\perp \vec{b} a ⊥ b ( 3 a ⃗ − b ⃗ ) ( a ⃗ + b ⃗ ) = 23 (3\vec{a}-\vec{b})(\vec{a}+\vec{b})=23 ( 3 a − b ) ( a + b ) = 2 3 a ⃗ ⊥ b ⃗ \vec{a}\perp \vec{b} a ⊥ b a ⃗ ⋅ b ⃗ = 0 \vec{a}\cdot \vec{b}=0 a ⋅ b = 0 3 a ⃗ 2 + 3 a ⃗ b ⃗ − b ⃗ ⋅ a ⃗ − b ⃗ 2 3\vec{a}^2 +3\vec{a}\vec{b}-\vec{b} \cdot \vec{a}-\vec{b}^2 3 a 2 + 3 a b − b ⋅ a − b 2 a ⃗ 2 = ∣ a ⃗ ∣ 2 \vec{a}^2=|\vec{a}|^2 a 2 = ∣ a ∣ 2 3 ⋅ 3 2 + 3 ⋅ 0 − 0 − 2 2 = 23 3\cdot 3^2+3\cdot 0-0-2^2=23 3 ⋅ 3 2 + 3 ⋅ 0 − 0 − 2 2 = 2 3
向量叉乘的运算 若a ⃗ = ( x 1 , y 1 , z 1 ) , b ⃗ = ( x 2 , y 2 , z 2 ) \vec{a}=(x_1,y_1,z_1),\vec{b}=(x_2,y_2,z_2) a = ( x 1 , y 1 , z 1 ) , b = ( x 2 , y 2 , z 2 ) a ⃗ × b ⃗ = ∣ i ⃗ j ⃗ k ⃗ x 1 y 1 z 1 x 2 y 2 z 2 ∣ \vec{a} \times \vec{b}=\begin{vmatrix}\vec{i} &\vec{j} &\vec{k} \\x_1 &y_1 &z_1 \\x_2 &y_2 &z_2 \\\end{vmatrix} a × b = ∣ ∣ ∣ ∣ ∣ ∣ ∣ i x 1 x 2 j y 1 y 2 k z 1 z 2 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ y 1 z 1 y 2 z 2 ∣ ⋅ i ⃗ − ∣ x 1 z 1 x 2 z 2 ∣ ⋅ j ⃗ + ∣ x 1 y 1 x 2 y 2 ∣ ⋅ k ⃗ \begin{vmatrix} y_1& z_1\\y_2&z_2\end{vmatrix}\cdot \vec{i}-\begin{vmatrix} x_1& z_1\\x_2&z_2\end{vmatrix}\cdot \vec{j}+\begin{vmatrix} x_1& y_1\\x_2&y_2\end{vmatrix}\cdot \vec{k} ∣ ∣ ∣ ∣ ∣ y 1 y 2 z 1 z 2 ∣ ∣ ∣ ∣ ∣ ⋅ i − ∣ ∣ ∣ ∣ ∣ x 1 x 2 z 1 z 2 ∣ ∣ ∣ ∣ ∣ ⋅ j + ∣ ∣ ∣ ∣ ∣ x 1 x 2 y 1 y 2 ∣ ∣ ∣ ∣ ∣ ⋅ k a ⃗ = ( 1 , 0 , − 1 ) , b ⃗ = ( 0 , 2 , 3 ) \vec{a}=(1,0,-1),\vec{b}=(0,2,3) a = ( 1 , 0 , − 1 ) , b = ( 0 , 2 , 3 ) a ⃗ × b ⃗ \vec{a}\times \vec{b} a × b a ⃗ × b ⃗ = ∣ i ⃗ j ⃗ k ⃗ 1 0 − 1 0 2 3 ∣ \vec{a} \times \vec{b}=\begin{vmatrix}\vec{i} &\vec{j} &\vec{k} \\1 &0 &-1 \\0 &2 &3 \\\end{vmatrix} a × b = ∣ ∣ ∣ ∣ ∣ ∣ ∣ i 1 0 j 0 2 k − 1 3 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 0 − 1 2 3 ∣ ⋅ i ⃗ − ∣ 1 − 1 0 3 ∣ ⋅ j ⃗ + ∣ 1 0 0 2 ∣ ⋅ k ⃗ \begin{vmatrix} 0& -1\\2&3 \end{vmatrix}\cdot \vec{i}-\begin{vmatrix} 1& -1\\0 &3 \end{vmatrix}\cdot \vec{j}+\begin{vmatrix} 1& 0\\0 & 2 \end{vmatrix}\cdot \vec{k} ∣ ∣ ∣ ∣ ∣ 0 2 − 1 3 ∣ ∣ ∣ ∣ ∣ ⋅ i − ∣ ∣ ∣ ∣ ∣ 1 0 − 1 3 ∣ ∣ ∣ ∣ ∣ ⋅ j + ∣ ∣ ∣ ∣ ∣ 1 0 0 2 ∣ ∣ ∣ ∣ ∣ ⋅ k = [ 0 − ( − 2 ) ] i ⃗ − ( 3 − 0 ) j ⃗ + ( 2 − 0 ) k ⃗ =[0-(-2)]\vec{i}-(3-0)\vec{j}+(2-0)\vec{k} = [ 0 − ( − 2 ) ] i − ( 3 − 0 ) j + ( 2 − 0 ) k = 2 i ⃗ − 3 j ⃗ + 2 k ⃗ =2\vec{i}-3\vec{j}+2\vec{k} = 2 i − 3 j + 2 k a ⃗ × b ⃗ = ( 2 , − 3 , 2 ) \vec{a} \times \vec{b}=(2,-3,2) a × b = ( 2 , − 3 , 2 ) 三阶行列式的计算方法 :D 3 = ∣ 1 2 0 0 1 0 1 1 2 ∣ D_3=\begin{vmatrix}1&2&0 \\0&1&0 \\1&1&2\end{vmatrix} D 3 = ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 0 1 2 1 1 0 0 2 ∣ ∣ ∣ ∣ ∣ ∣ ∣ 主对角-副对角,即捺-撇;= ∣ 1 2 0 0 1 0 1 1 2 ∣ 1 2 0 1 1 1 =\begin{vmatrix}1&2&0 \\0&1&0 \\1&1&2\end{vmatrix}{\color{Red} \begin{matrix}1&2 \\0&1 \\1&1\end{matrix}} = ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 0 1 2 1 1 0 0 2 ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 0 1 2 1 1 = ( 2 + 0 + 0 ) − ( 0 + 0 + 0 ) = 2 =(2+0+0)-(0+0+0)=2 = ( 2 + 0 + 0 ) − ( 0 + 0 + 0 ) = 2 某一表白公式 例题1使用对角线法解题
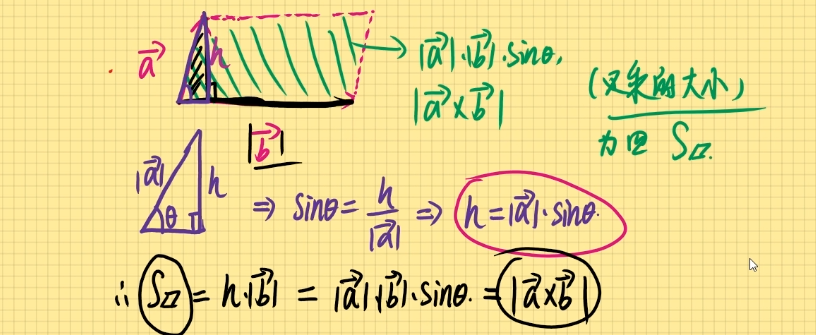
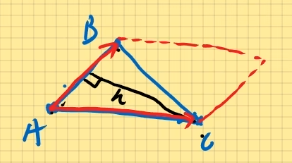
a ⃗ × b ⃗ \vec{a}\times \vec{b} a × b ∣ a ⃗ × b ⃗ ∣ = ∣ a ⃗ ∣ ⋅ ∣ b ⃗ ∣ ⋅ sin θ |\vec{a}\times \vec{b}|=|\vec{a}|\cdot |\vec{b}|\cdot \sin \theta ∣ a × b ∣ = ∣ a ∣ ⋅ ∣ b ∣ ⋅ sin θ 几何意义:指由a ⃗ , b ⃗ \vec{a},\vec{b} a , b 1 2 ∣ a ⃗ × b ⃗ ∣ \frac{1}{2}|\vec{a}\times \vec{b}| 2 1 ∣ a × b ∣ △ A B C \bigtriangleup ABC △ A B C A ( 1 , 2 , 3 ) , B ( 3 , − 1 , 2 ) , C ( 1 , 3 , 2 ) A(1,2,3),B(3,-1,2),C(1,3,2) A ( 1 , 2 , 3 ) , B ( 3 , − 1 , 2 ) , C ( 1 , 3 , 2 ) h = 2 21 7 h=\frac{2\sqrt{21} }{7} h = 7 2 2 1 A B ⃗ = ( 3 − 1 , − 1 − 2 , 2 − 3 ) = ( 2 , − 3 , − 1 ) \vec{AB}=(3-1,-1-2,2-3)=(2,-3,-1) A B = ( 3 − 1 , − 1 − 2 , 2 − 3 ) = ( 2 , − 3 , − 1 ) A C ⃗ = ( 1 − 1 , 3 − 2 , 2 − 3 ) = ( 0 , 1 , − 1 ) \vec{AC}=(1-1,3-2,2-3)=(0,1,-1) A C = ( 1 − 1 , 3 − 2 , 2 − 3 ) = ( 0 , 1 , − 1 ) ∣ A B ⃗ × A C ⃗ ∣ = ∣ i ⃗ j ⃗ k ⃗ 2 − 3 − 1 0 1 − 1 ∣ |\vec{AB}\times \vec{AC}|=\begin{vmatrix}\vec{i} &\vec{j} &\vec{k} \\2 &-3 &-1 \\0 &1 &-1 \\\end{vmatrix} ∣ A B × A C ∣ = ∣ ∣ ∣ ∣ ∣ ∣ ∣ i 2 0 j − 3 1 k − 1 − 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ = ( 3 i ⃗ + 0 + 2 k ⃗ − ( 0 − i ⃗ − 2 j ⃗ ) =(3\vec{i}+0+2\vec{k}-(0-\vec{i}-2\vec{j}) = ( 3 i + 0 + 2 k − ( 0 − i − 2 j ) = 4 i ⃗ + 2 j ⃗ + 2 k ⃗ = ( 4 , 2 , 2 ) =4\vec{i}+2\vec{j}+2\vec{k}=(4,2,2) = 4 i + 2 j + 2 k = ( 4 , 2 , 2 ) ∣ A B ⃗ × A C ⃗ ∣ = 4 2 + 2 2 + 2 2 = 24 = 2 6 |\vec{AB}\times \vec{AC}|=\sqrt{4^2+2^2+2^2}=\sqrt{24}=2\sqrt{6} ∣ A B × A C ∣ = 4 2 + 2 2 + 2 2 = 2 4 = 2 6 S △ = 1 2 ∣ A B ⃗ × A C ⃗ ∣ = 1 2 ⋅ 2 6 = 6 S_\bigtriangleup =\frac{1}{2}|\vec{AB}\times \vec{AC}|=\frac{1}{2} \cdot 2\sqrt{6}=\sqrt{6} S △ = 2 1 ∣ A B × A C ∣ = 2 1 ⋅ 2 6 = 6 A B ⃗ = 2 2 + ( − 3 ) 2 + ( − 1 ) 2 = 14 \vec{AB}=\sqrt{2^2+(-3)^2+(-1)^2}=\sqrt{14} A B = 2 2 + ( − 3 ) 2 + ( − 1 ) 2 = 1 4 h = S △ ⋅ 2 A B ⃗ = 2 6 14 h=\frac{S_\bigtriangleup \cdot 2}{\vec{AB}}=\frac{2\sqrt{6} }{\sqrt{14} } h = A B S △ ⋅ 2 = 1 4 2 6 h = 2 21 7 h=\frac{2\sqrt{21} }{7} h = 7 2 2 1
向量间位置关系 设a ⃗ = ( x 1 , y 1 , z 1 ) , b ⃗ = ( x 2 , y 2 , z 2 ) \vec{a}=(x_1,y_1,z_1),\vec{b}=(x_2,y_2,z_2) a = ( x 1 , y 1 , z 1 ) , b = ( x 2 , y 2 , z 2 ) a ⃗ ⊥ b ⃗ ⇔ a ⃗ ⋅ b ⃗ \vec{a}\perp \vec{b} \Leftrightarrow \vec{a}\cdot \vec{b} a ⊥ b ⇔ a ⋅ b a ⃗ ∥ b ⃗ ⇔ x 1 x 2 = y 1 y 2 = z 1 z 2 \vec{a}\parallel \vec{b} \Leftrightarrow \frac{x_1}{x_2}=\frac{y_1}{y_2}=\frac{z_1}{z_2} a ∥ b ⇔ x 2 x 1 = y 2 y 1 = z 2 z 1 a ⃗ = ( 5 , x , − 2 ) , b ⃗ = ( y , 6 , 4 ) \vec{a}=(5,x,-2),\vec{b}=(y,6,4) a = ( 5 , x , − 2 ) , b = ( y , 6 , 4 ) x = ( ) , y = ( ) x=(),y=() x = ( ) , y = ( ) a ⃗ ∥ b ⃗ \vec{a}\parallel \vec{b} a ∥ b 5 y = x 6 = − 2 4 \frac{5}{y}=\frac{x}{6}=\frac{-2}{4} y 5 = 6 x = 4 − 2 x = − 3 , y = − 10 x=-3,y=-10 x = − 3 , y = − 1 0
空间平面方程
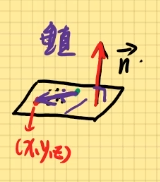
点法式方程: A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 A(x-x_0)+B(y_-y_0)+C(z-z_0)=0 A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 n ⃗ = ( A , B , C ) \vec{n}=(A,B,C) n = ( A , B , C ) M ( x , y , z ) , M 0 ( x 0 , y 0 , z 0 ) M(x,y,z),M_0(x_0,y_0,z_0) M ( x , y , z ) , M 0 ( x 0 , y 0 , z 0 ) M 0 M ⃗ = ( x − x 0 , y − y 0 , z − z 0 ) \vec{M_0M}=(x-x_0,y-y_0,z-z_0) M 0 M = ( x − x 0 , y − y 0 , z − z 0 ) n ⃗ ⊥ M 0 M ⃗ \vec{n} \perp \vec{M_0M} n ⊥ M 0 M n ⃗ ⋅ M 0 M ⃗ = 0 \vec{n} \cdot \vec{M_0M}=0 n ⋅ M 0 M = 0 A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 A(x-x_0)+B(y-y_0)+C(z-z_0)=0 A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0
一般式方程(点法式展开):A x + B y + C z + D = 0 Ax+By+Cz+D=0 A x + B y + C z + D = 0
空间平面位置关系 设有两个平面:π 1 : A 1 x + B 1 y + C 1 z + D 1 = 0 \pi _1:A_1x+B_1y+C_1z+D_1=0 π 1 : A 1 x + B 1 y + C 1 z + D 1 = 0 π 2 : A 2 x + B 2 y + C 2 z + D 2 = 0 \pi _2:A_2x+B_2y+C_2z+D_2=0 π 2 : A 2 x + B 2 y + C 2 z + D 2 = 0 n 1 ⃗ = ( A 1 , B 1 , C 1 ) ; n 2 ⃗ = ( A 2 , B 2 , C 2 ) \vec{n_1}=(A_1,B_1,C_1);\vec{n_2}=(A_2,B_2,C_2) n 1 = ( A 1 , B 1 , C 1 ) ; n 2 = ( A 2 , B 2 , C 2 )
平行:π 1 ∥ π 2 ⇔ n 1 ⃗ ∥ n 2 ⃗ ⇔ A 1 A 2 = B 1 B 2 = C 1 C 2 \pi _1 \parallel \pi _2 \Leftrightarrow \vec{n_1} \parallel \vec{n_2} \Leftrightarrow \frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2} π 1 ∥ π 2 ⇔ n 1 ∥ n 2 ⇔ A 2 A 1 = B 2 B 1 = C 2 C 1
垂直:π 1 ⊥ π 2 ⇔ n 1 ⃗ ⊥ n 2 ⃗ ⇔ n 1 ⃗ ⋅ n 2 ⃗ = 0 ⇔ A 1 ⋅ A 2 + B 1 ⋅ B 2 + C 1 ⋅ C 2 = 0 \pi _1 \perp \pi _2 \Leftrightarrow \vec{n_1} \perp \vec{n_2} \Leftrightarrow \vec{n_1} \cdot \vec{n_2}=0 \Leftrightarrow A_1\cdot A_2+B_1\cdot B_2+C_1\cdot C_2=0 π 1 ⊥ π 2 ⇔ n 1 ⊥ n 2 ⇔ n 1 ⋅ n 2 = 0 ⇔ A 1 ⋅ A 2 + B 1 ⋅ B 2 + C 1 ⋅ C 2 = 0
相交:A 1 A 2 = B 1 B 2 = C 1 C 2 \frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2} A 2 A 1 = B 2 B 1 = C 2 C 1
重合:{ 平行 有交点 } ⟹ A 1 A 2 = B 1 B 2 = C 1 C 2 = D 1 D 2 \begin{Bmatrix}平行\\有交点\end{Bmatrix}\Longrightarrow \frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}=\frac{D_1}{D_2} { 平 行 有 交 点 } ⟹ A 2 A 1 = B 2 B 1 = C 2 C 1 = D 2 D 1 n 1 ⃗ , n 2 ⃗ \vec{n_1},\vec{n_2} n 1 , n 2 π 1 : x − 5 y + 2 z = − 1 \pi _1:x-5y+2z=-1 π 1 : x − 5 y + 2 z = − 1 π 2 : 3 x − 2 y + 5 z + 8 = 0 \pi _2:3x-2y+5z+8=0 π 2 : 3 x − 2 y + 5 z + 8 = 0 π 3 : 4 x + 2 y + 3 z − 9 = 0 \pi _3:4x+2y+3z-9=0 π 3 : 4 x + 2 y + 3 z − 9 = 0 π 1 , π 2 , π 3 \pi _1,\pi _2,\pi _3 π 1 , π 2 , π 3 π 1 ∥ π 2 \pi _1 \parallel \pi _2 π 1 ∥ π 2 π 1 ⊥ π 3 \pi _1 \perp \pi _3 π 1 ⊥ π 3 π 2 ⊥ π 3 \pi _2 \perp \pi _3 π 2 ⊥ π 3 π 2 ∥ π 3 \pi _2 \parallel \pi _3 π 2 ∥ π 3 n 1 ⃗ = ( 1 , − 5 , 2 ) ; n 2 ⃗ = ( 3 , − 2 , 5 ) ; n 3 ⃗ = ( 4 , 2 , 3 ) \vec{n_1}=(1,-5,2);\vec{n_2}=(3,-2,5);\vec{n_3}=(4,2,3) n 1 = ( 1 , − 5 , 2 ) ; n 2 = ( 3 , − 2 , 5 ) ; n 3 = ( 4 , 2 , 3 ) n 1 ⃗ ∥ n 2 ⃗ = 1 3 ≠ 5 2 ≠ 2 5 \vec{n_1} \parallel \vec{n_2}=\frac{1}{3}\neq \frac{5}{2}\neq \frac{2}{5} n 1 ∥ n 2 = 3 1 = 2 5 = 5 2 n 1 ⃗ ⋅ n 3 ⃗ = 1 ⋅ 4 + ( − 5 ) ⋅ 2 + 2 ⋅ 3 = 0 \vec{n_1} \cdot \vec{n_3}=1\cdot 4+(-5)\cdot 2+2\cdot 3=0 n 1 ⋅ n 3 = 1 ⋅ 4 + ( − 5 ) ⋅ 2 + 2 ⋅ 3 = 0 n 2 ⃗ ⋅ n 3 ⃗ = 3 ⋅ 4 + ( − 2 ) ⋅ 2 + 5 ⋅ 3 ≠ 0 \vec{n_2} \cdot \vec{n_3}=3\cdot 4+(-2)\cdot 2+5\cdot 3\neq 0 n 2 ⋅ n 3 = 3 ⋅ 4 + ( − 2 ) ⋅ 2 + 5 ⋅ 3 = 0 n 2 ⃗ ∥ n 3 ⃗ = 3 4 ≠ − 2 2 ≠ 5 3 \vec{n_2} \parallel \vec{n_3}=\frac{3}{4}\neq \frac{-2}{2}\neq \frac{5}{3} n 2 ∥ n 3 = 4 3 = 2 − 2 = 3 5 找目标条件 { 1. 平面上一点 ( x 0 , y 0 , z 0 ) 2. 平面 n ⃗ ( A , B , C ) 找目标条件\left\{\begin{matrix}1. 平面上一点(x_0,y_0,z_0)\\2. 平面\vec{n}(A,B,C) \end{matrix}\right. 找 目 标 条 件 { 1 . 平 面 上 一 点 ( x 0 , y 0 , z 0 ) 2 . 平 面 n ( A , B , C ) A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 A(x-x_0)+B(y-y_0)+C(z-z_0)=0 A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 M ( 1 , 2 , 3 ) M(1,2,3) M ( 1 , 2 , 3 ) n ⃗ = ( 4 , 5 , 6 ) \vec{n}=(4,5,6) n = ( 4 , 5 , 6 ) A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 A(x-x_0)+B(y-y_0)+C(z-z_0)=0 A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 4 ( x − 1 ) + 5 ( y − 2 ) + 6 ( z − 3 ) = 0 4(x-1)+5(y-2)+6(z-3)=0 4 ( x − 1 ) + 5 ( y − 2 ) + 6 ( z − 3 ) = 0 4 x + 5 y + 6 z − 32 = 0 4x+5y+6z-32=0 4 x + 5 y + 6 z − 3 2 = 0 A ( 1 , 1 , 1 ) , B ( 0 , 1 , − 1 ) A(1,1,1),B(0,1,-1) A ( 1 , 1 , 1 ) , B ( 0 , 1 , − 1 ) x + y + z = 0 x+y+z=0 x + y + z = 0 n 1 ⃗ ⊥ n 2 ⃗ ⟹ n 1 ⃗ × n 2 ⃗ = 0 \vec{n_1}\perp \vec{n_2}\Longrightarrow \vec{n_1}\times \vec{n_2}=0 n 1 ⊥ n 2 ⟹ n 1 × n 2 = 0 c ⃗ ⊥ a ⃗ c ⃗ ⊥ b ⃗ ⟹ c ⃗ = a ⃗ × b ⃗ \begin{matrix}\vec{c}\perp \vec{a}\\ \vec{c}\perp \vec{b}\end{matrix}\Longrightarrow \vec{c}=\vec{a}\times \vec{b} c ⊥ a c ⊥ b ⟹ c = a × b A B ⃗ = ( − 1 , 0 , − 2 ) \vec{AB}=(-1,0,-2) A B = ( − 1 , 0 , − 2 ) n 1 ⃗ \vec{n_1} n 1 n 1 ⃗ ⊥ A B ⃗ \vec{n_1}\perp \vec{AB} n 1 ⊥ A B x + y + z = 0 x+y+z=0 x + y + z = 0 n 2 ⃗ = ( 1 , 1 , 1 ) \vec{n_2}=(1,1,1) n 2 = ( 1 , 1 , 1 ) n 1 ⃗ ⊥ n 2 ⃗ \vec{n_1}\perp \vec{n_2} n 1 ⊥ n 2 n 1 ⃗ = A B ⃗ × n 2 ⃗ \vec{n_1}=\vec{AB}\times \vec{n_2} n 1 = A B × n 2 n 1 ⃗ = ∣ i ⃗ j ⃗ k ⃗ − 1 0 − 2 1 1 1 ∣ i ⃗ j ⃗ − 1 0 1 1 \vec{n_1}=\begin{vmatrix}\vec{i} &\vec{j} &\vec{k} \\-1&0&-2\\1&1&1\end{vmatrix}{\color{Red} \begin{matrix}\vec{i} &\vec{j} \\-1&0\\1&1\end{matrix}} n 1 = ∣ ∣ ∣ ∣ ∣ ∣ ∣ i − 1 1 j 0 1 k − 2 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ i − 1 1 j 0 1 = ( 0 − 2 j ⃗ − k ⃗ ) − ( 0 − 2 i ⃗ + j ⃗ ) = ( 2 , − 1 , − 1 ) =(0-2\vec{j}-\vec{k})-(0-2\vec{i}+\vec{j})=(2,-1,-1) = ( 0 − 2 j − k ) − ( 0 − 2 i + j ) = ( 2 , − 1 , − 1 ) A ( 1 , 1 , 1 ) A(1,1,1) A ( 1 , 1 , 1 ) 1 ⋅ 2 + 1 ⋅ ( − 1 ) + 1 ⋅ ( − 1 ) = 0 1\cdot 2+1\cdot (-1)+1\cdot (-1)=0 1 ⋅ 2 + 1 ⋅ ( − 1 ) + 1 ⋅ ( − 1 ) = 0 2 x − y − z = 0 2x-y-z=0 2 x − y − z = 0
空间平面的夹角及点面距离公式
平面间的夹角:{ 1. 找 n 1 ⃗ , n 2 ⃗ 2. 求 cos θ = n 1 ⃗ ⋅ n 2 ⃗ ∣ n 1 ⃗ ∣ ⋅ ∣ n 2 ⃗ ∣ 3. 反推 θ 大小 \left\{\begin{matrix}1. 找\vec{n_1},\vec{n_2} \\2. 求\cos \theta =\frac{\vec{n_1}\cdot \vec{n_2} }{|\vec{n_1} |\cdot |\vec{n_2} |} \\3. 反推\theta 大小\end{matrix}\right. ⎩ ⎪ ⎨ ⎪ ⎧ 1 . 找 n 1 , n 2 2 . 求 cos θ = ∣ n 1 ∣ ⋅ ∣ n 2 ∣ n 1 ⋅ n 2 3 . 反 推 θ 大 小
点到平面的距离:P ( x 0 , y 0 , z 0 ) P(x_0,y_0,z_0) P ( x 0 , y 0 , z 0 ) π : A x + B y + C z + D = 0 \pi :Ax+By+Cz+D=0 π : A x + B y + C z + D = 0 d = ∣ A x 0 + B y 0 + C z 0 + D ∣ A 2 + B 2 + C 2 d=\frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}} d = A 2 + B 2 + C 2 ∣ A x 0 + B y 0 + C z 0 + D ∣ M ( 1 , 2 , 3 ) M(1,2,3) M ( 1 , 2 , 3 ) π : x + y + 2 z + 3 = 0 \pi :x+y+2z+3=0 π : x + y + 2 z + 3 = 0 d = ∣ A x 0 + B y 0 + C z 0 + D ∣ A 2 + B 2 + C 2 d=\frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}} d = A 2 + B 2 + C 2 ∣ A x 0 + B y 0 + C z 0 + D ∣ d = ∣ 1 + 2 + 2 ⋅ 3 + 3 ∣ 1 2 + 1 2 + 2 2 = 12 8 = 6 2 d=\frac{|1+2+2\cdot 3+3|}{\sqrt{1^2+1^2+2^2}}=\frac{12}{\sqrt{8}}=\frac{\sqrt{6} }{2} d = 1 2 + 1 2 + 2 2 ∣ 1 + 2 + 2 ⋅ 3 + 3 ∣ = 8 1 2 = 2 6
特殊平面方程 平面的一般式方程:A x + B y + C z + D = 0 Ax+By+Cz+D=0 A x + B y + C z + D = 0
D = 0 , A x + B y + C z + D = 0 D=0,Ax+By+Cz+D=0 D = 0 , A x + B y + C z + D = 0 少某个字母(x , y , z x,y,z x , y , z z , A x + B y + D = 0 ( z ∈ R ) z,Ax+By+D=0 (z \in R) z , A x + B y + D = 0 ( z ∈ R )
少了两个字母(z , y z,y z , y z , y , A x + D = 0 ( z , y ∈ R ) z,y,Ax+D=0 (z,y \in R) z , y , A x + D = 0 ( z , y ∈ R )
少了某个字母和某个系数(z , D z,D z , D A x + B y = 0 Ax+By=0 A x + B y = 0 M 0 ( − 3 , 1 , 2 ) M_0(-3,1,2) M 0 ( − 3 , 1 , 2 ) A x + B y = 0 Ax+By=0 A x + B y = 0 M 0 ( − 3 , 1 , 2 ) M_0(-3,1,2) M 0 ( − 3 , 1 , 2 ) A ⋅ ( − 3 ) + B ⋅ 1 = 0 A\cdot (-3)+B\cdot 1=0 A ⋅ ( − 3 ) + B ⋅ 1 = 0 A = B 3 A=\frac{B}{3} A = 3 B B = 3 B=3 B = 3 A = 1 A=1 A = 1 x + 3 y = 0 x+3y=0 x + 3 y = 0
空间直线方程
直线的点向式方程:x − x 0 m = y − y 0 n = z − z 0 p \frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p} m x − x 0 = n y − y 0 = p z − z 0 S ⃗ = ( m , n , p ) \vec{S}=(m,n,p) S = ( m , n , p ) M ( x , y , z ) , M 0 ( x 0 , y 0 , z 0 ) M(x,y,z),M_0(x_0,y_0,z_0) M ( x , y , z ) , M 0 ( x 0 , y 0 , z 0 ) M 0 M M_0M M 0 M M 0 M ⃗ = ( x − x 0 , y − y 0 , z − z 0 ) \vec{M_0M}=(x-x_0,y-y_0,z-z_0) M 0 M = ( x − x 0 , y − y 0 , z − z 0 ) M 0 M ⃗ ∥ S ⃗ \vec{M_0M} \parallel \vec{S} M 0 M ∥ S x − x 0 m = y − y 0 n = z − z 0 p \frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p} m x − x 0 = n y − y 0 = p z − z 0 看分母,得S ⃗ = ( m , n , p ) \vec{S}=(m,n,p) S = ( m , n , p ) 看分子,得点M ( x 0 , y 0 , z 0 ) M(x_0,y_0,z_0) M ( x 0 , y 0 , z 0 )
参数方程x − x 0 m = y − y 0 n = z − z 0 p = t \frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p}=t m x − x 0 = n y − y 0 = p z − z 0 = t { x = x 0 + m t y = y 0 + n t z = z 0 + p t \left\{\begin{matrix}x=x_0+mt\\y=y_0+nt\\z=z_0+pt\end{matrix}\right. ⎩ ⎪ ⎨ ⎪ ⎧ x = x 0 + m t y = y 0 + n t z = z 0 + p t 交点使用参数方程。
直线的一般式方程(交面式){ A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 \left\{\begin{matrix}A_1x+B_1y+C_1z+D_1=0\\A_2x+B_2y+C_2z+D_2=0\end{matrix}\right. { A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0
直线与直线的位置关系 设两直线方程为:{ l 1 : x − x 1 m 1 = y − y 1 n 1 = z − z 1 p 1 l 2 : x − x 2 m 2 = y − y 2 n 2 = z − z 2 p 2 \left\{\begin{matrix}l_1:\frac{x-x_1}{m_1}=\frac{y-y_1}{n_1}=\frac{z-z_1}{p_1}\\l_2:\frac{x-x_2}{m_2}=\frac{y-y_2}{n_2}=\frac{z-z_2}{p_2}\end{matrix}\right. { l 1 : m 1 x − x 1 = n 1 y − y 1 = p 1 z − z 1 l 2 : m 2 x − x 2 = n 2 y − y 2 = p 2 z − z 2 S 1 ⃗ = ( m 1 , n 1 , p 1 ) ; S 2 ⃗ = ( m 2 , n 2 , p 2 ) \vec{S_1}=(m_1,n_1,p_1);\vec{S_2}=(m_2,n_2,p_2) S 1 = ( m 1 , n 1 , p 1 ) ; S 2 = ( m 2 , n 2 , p 2 )
平行:S 1 ⃗ ∥ S 2 ⃗ \vec{S_1} \parallel \vec{S_2} S 1 ∥ S 2
垂直:S 1 ⃗ ⊥ S 2 ⃗ \vec{S_1} \perp \vec{S_2} S 1 ⊥ S 2
重合:{ 1. 平行 2. 有交点 \left\{\begin{matrix}1. 平行\\2. 有交点\end{matrix}\right. { 1 . 平 行 2 . 有 交 点 线和线的位置关系与向量关系一致 。
直线与平面的位置关系 与向量的位置关系相反。π : A x + B y + C z + D = 0 \pi :Ax+By+Cz+D=0 π : A x + B y + C z + D = 0 l : x − x 0 m = y − y 0 n = z − z 0 p l:\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p} l : m x − x 0 = n y − y 0 = p z − z 0 n ⃗ = ( A , B , C ) ; S ⃗ = ( m , n , p ) \vec{n}=(A,B,C);\vec{S}=(m,n,p) n = ( A , B , C ) ; S = ( m , n , p )
平行:n ⃗ ⊥ S ⃗ \vec{n} \perp \vec{S} n ⊥ S
垂直:n ⃗ ∥ S ⃗ \vec{n} \parallel \vec{S} n ∥ S
重合:{ 1. 平行 2. 直线上的点 ( x 0 , y 0 , z 0 ) 在平面上 \left\{\begin{matrix}1. 平行\\2. 直线上的点(x_0,y_0,z_0)在平面上\end{matrix}\right. { 1 . 平 行 2 . 直 线 上 的 点 ( x 0 , y 0 , z 0 ) 在 平 面 上
例题
直线与直线的位置关系l 1 : x + 14 3 = y 1 = z + 21 5 l_1:\frac{x+14}{3}=\frac{y}{1}=\frac{z+21}{5} l 1 : 3 x + 1 4 = 1 y = 5 z + 2 1 { x = 1 3 − 9 t y = 1 − 3 t z = 1 − 3 − 15 t \left\{\begin{matrix}x=\frac{1}{3}-9t \\y=1-3t\\z=\frac{1}{-3}-15t \end{matrix}\right. ⎩ ⎪ ⎨ ⎪ ⎧ x = 3 1 − 9 t y = 1 − 3 t z = − 3 1 − 1 5 t S 1 ⃗ = ( 3 , 1 , 5 ) ; S 2 ⃗ = ( − 9 , − 3 , − 15 ) \vec{S_1}=(3,1,5);\vec{S_2}=(-9,-3,-15) S 1 = ( 3 , 1 , 5 ) ; S 2 = ( − 9 , − 3 , − 1 5 ) ∵ 3 − 9 = 1 − 3 = 5 − 15 = − 1 3 \because \frac{3}{-9}=\frac{1}{-3}=\frac{5}{-15}=-\frac{1}{3} ∵ − 9 3 = − 3 1 = − 1 5 5 = − 3 1 ∴ S 1 ⃗ ∥ S 2 ⃗ \therefore \vec{S_1} \parallel \vec{S_2} ∴ S 1 ∥ S 2 l 2 l_2 l 2 ( 1 3 , 1 , − 1 3 ) (\frac{1}{3},1,-\frac{1}{3}) ( 3 1 , 1 , − 3 1 ) l 1 l_1 l 1
直线与平面的位置关系l : x 2 = y − 5 5 = z − 6 3 l:\frac{x}{2}=\frac{y-5}{5}=\frac{z-6}{3} l : 2 x = 5 y − 5 = 3 z − 6 π : 15 x − 9 y + 5 z = − 15 \pi :15x-9y+5z=-15 π : 1 5 x − 9 y + 5 z = − 1 5 n ⃗ = ( 15 , − 9 , 5 ) ; S ⃗ = ( 2 , 5 , 3 ) \vec{n}=(15,-9,5);\vec{S}=(2,5,3) n = ( 1 5 , − 9 , 5 ) ; S = ( 2 , 5 , 3 ) 2 15 ≠ 5 − 9 ≠ 3 5 \frac{2}{15}\neq \frac{5}{-9}\neq \frac{3}{5} 1 5 2 = − 9 5 = 5 3 n ⃗ ⋅ S ⃗ = 15 ⋅ 2 + ( − 9 ) ⋅ 5 + 5 ⋅ 3 = 0 \vec{n} \cdot \vec{S}=15\cdot 2+(-9)\cdot 5+5\cdot 3=0 n ⋅ S = 1 5 ⋅ 2 + ( − 9 ) ⋅ 5 + 5 ⋅ 3 = 0 ∴ n ⃗ ⊥ S ⃗ \therefore \vec{n} \perp \vec{S} ∴ n ⊥ S l ∥ π l \parallel \pi l ∥ π M 0 ( 0 , 5 , 6 ) M_0(0,5,6) M 0 ( 0 , 5 , 6 )
求平面与直线的交点坐标x − 2 3 = y 2 = z − 1 5 \frac{x-2}{3}=\frac{y}{2}=\frac{z-1}{5} 3 x − 2 = 2 y = 5 z − 1 x + y + z + 2 = 0 x+y+z+2=0 x + y + z + 2 = 0 x − 2 3 = y 2 = z − 1 5 = t \frac{x-2}{3}=\frac{y}{2}=\frac{z-1}{5}=t 3 x − 2 = 2 y = 5 z − 1 = t { x = 2 + 3 t y = 2 t z = 1 + 5 t \left\{\begin{matrix}x=2+3t\\y=2t\\z=1+5t\end{matrix}\right. ⎩ ⎪ ⎨ ⎪ ⎧ x = 2 + 3 t y = 2 t z = 1 + 5 t 2 + 3 t + 2 t + 1 + 5 t + 2 = 0 2+3t+2t+1+5t+2=0 2 + 3 t + 2 t + 1 + 5 t + 2 = 0 10 t = − 5 10t=-5 1 0 t = − 5 t = − 1 2 t=-\frac{1}{2} t = − 2 1 t = − 1 2 t=-\frac{1}{2} t = − 2 1 x = 2 + 3 ⋅ ( − 1 2 ) = 1 2 x=2+3\cdot (-\frac{1}{2})=\frac{1}{2} x = 2 + 3 ⋅ ( − 2 1 ) = 2 1 y = 2 ⋅ ( − 1 2 ) = − 1 y=2\cdot (-\frac{1}{2})=-1 y = 2 ⋅ ( − 2 1 ) = − 1 z = 1 + 5 ⋅ ( − 1 2 ) = − 3 2 z=1+5\cdot (-\frac{1}{2})=-\frac{3}{2} z = 1 + 5 ⋅ ( − 2 1 ) = − 2 3 M ( 1 2 , − 1 , − 3 2 ) M(\frac{1}{2},-1,-\frac{3}{2}) M ( 2 1 , − 1 , − 2 3 ) A ( 2 , − 1 , 3 ) A(2,-1,3) A ( 2 , − 1 , 3 ) x − 2 y − 2 z + 11 = 0 x-2y-2z+11=0 x − 2 y − 2 z + 1 1 = 0 B ( x 0 , y 0 , z 0 ) B(x_0,y_0,z_0) B ( x 0 , y 0 , z 0 ) n ⃗ = ( 1 , − 2 , − 2 ) \vec{n}=(1,-2,-2) n = ( 1 , − 2 , − 2 ) S ⃗ = ( 1 , − 2 , − 2 ) \vec{S}=(1,-2,-2) S = ( 1 , − 2 , − 2 ) x − 2 1 = y + 1 − 2 = z − 3 − 2 = t \frac{x-2}{1}=\frac{y+1}{-2}=\frac{z-3}{-2}=t 1 x − 2 = − 2 y + 1 = − 2 z − 3 = t { x = t + 2 y = − 2 t − 1 z = − 2 t + 3 \left\{\begin{matrix}x=t+2\\y=-2t-1\\z=-2t+3\end{matrix}\right. ⎩ ⎪ ⎨ ⎪ ⎧ x = t + 2 y = − 2 t − 1 z = − 2 t + 3 x − 2 y − 2 z + 11 = 0 x-2y-2z+11=0 x − 2 y − 2 z + 1 1 = 0 t + 2 − 2 ( − 2 t − 1 ) − 2 ( − 2 t + 3 ) + 11 = 0 t+2-2(-2t-1)-2(-2t+3)+11=0 t + 2 − 2 ( − 2 t − 1 ) − 2 ( − 2 t + 3 ) + 1 1 = 0 t = − 1 t=-1 t = − 1 t = 1 t=1 t = 1 ( 1 , 1 , 5 ) (1,1,5) ( 1 , 1 , 5 )
直线与直线的夹角θ \theta θ (1). 找两个直线的方向向量S 1 ⃗ , S 2 ⃗ \vec{S_1},\vec{S_2} S 1 , S 2 cos θ = S 1 ⃗ ⋅ S 2 ⃗ ∣ S 1 ⃗ ∣ ⋅ ∣ S 2 ⃗ ∣ \cos \theta =\frac{\vec{S_1}\cdot \vec{S_2} }{|\vec{S_1} |\cdot |\vec{S_2} |} cos θ = ∣ S 1 ∣ ⋅ ∣ S 2 ∣ S 1 ⋅ S 2 θ \theta θ l 1 : x − 1 1 = y − 5 − 2 = z + 8 1 l_1:\frac{x-1}{1}=\frac{y-5}{-2}=\frac{z+8}{1} l 1 : 1 x − 1 = − 2 y − 5 = 1 z + 8 { x = t + 6 y = t z = − 2 t + 3 \left\{\begin{matrix}x=t+6\\y=t\\z=-2t+3\end{matrix}\right. ⎩ ⎪ ⎨ ⎪ ⎧ x = t + 6 y = t z = − 2 t + 3 π 3 \frac{\pi }{3} 3 π π 4 \frac{\pi }{4} 4 π π 6 \frac{\pi }{6} 6 π π 2 \frac{\pi }{2} 2 π S 1 ⃗ = ( 1 , − 2 , 1 ) ; S 2 ⃗ = ( 1 , 1 , − 2 ) \vec{S_1}=(1,-2,1);\vec{S_2}=(1,1,-2) S 1 = ( 1 , − 2 , 1 ) ; S 2 = ( 1 , 1 , − 2 ) cos θ = ∣ S 1 ⃗ ⋅ S 2 ⃗ ∣ S 1 ⃗ ∣ ⋅ ∣ S 2 ⃗ ∣ ∣ \cos \theta =|\frac{\vec{S_1} \cdot \vec{S_2} }{|\vec{S_1}|\cdot |\vec{S_2}|}| cos θ = ∣ ∣ S 1 ∣ ⋅ ∣ S 2 ∣ S 1 ⋅ S 2 ∣ = ∣ 1 ⋅ 1 + ( − 2 ) ⋅ 1 + 1 ⋅ ( − 2 ) 1 2 + ( − 2 ) 2 + 1 2 ⋅ 1 2 + 1 2 + ( − 2 ) 2 ∣ = 3 6 ⋅ 6 = 3 6 = 1 2 =|\frac{1\cdot 1+(-2)\cdot 1+1\cdot (-2)}{\sqrt{1^2+(-2)^2+1^2}\cdot \sqrt{1^2+1^2+(-2)^2}}|=\frac{3}{\sqrt{6} \cdot \sqrt{6} }=\frac{3}{6}=\frac{1}{2} = ∣ 1 2 + ( − 2 ) 2 + 1 2 ⋅ 1 2 + 1 2 + ( − 2 ) 2 1 ⋅ 1 + ( − 2 ) ⋅ 1 + 1 ⋅ ( − 2 ) ∣ = 6 ⋅ 6 3 = 6 3 = 2 1 ∴ θ = π 3 \therefore \theta =\frac{\pi }{3} ∴ θ = 3 π
向量的方向角 正向或基向量 的交角称为向量的方向角,向量的方向角的余弦称为向量的方向余弦。r = x i + y j + z k r=xi+y j+zk r = x i + y j + z k α , β , γ \alpha ,\beta ,\gamma α , β , γ cos α = r ⋅ i ∣ r ∣ = x x 2 + y 2 + z 2 \cos \alpha =\frac{r \cdot i}{|r|}=\frac{x}{\sqrt{x^2+y^2+z^2}} cos α = ∣ r ∣ r ⋅ i = x 2 + y 2 + z 2 x cos β = r ⋅ j ∣ r ∣ = y x 2 + y 2 + z 2 \cos \beta =\frac{r \cdot j}{|r|}=\frac{y}{\sqrt{x^2+y^2+z^2}} cos β = ∣ r ∣ r ⋅ j = x 2 + y 2 + z 2 y cos γ = r ⋅ z ∣ r ∣ = z x 2 + y 2 + z 2 \cos \gamma =\frac{r \cdot z}{|r|}=\frac{z}{\sqrt{x^2+y^2+z^2}} cos γ = ∣ r ∣ r ⋅ z = x 2 + y 2 + z 2 z cos 2 α + cos 2 β + cos 2 γ = 1 \cos ^2 \alpha +\cos ^2 \beta +\cos ^2 \gamma =1 cos 2 α + cos 2 β + cos 2 γ = 1 r = ∣ r ∣ ( cos α , cos β , cos γ ) r=|r|(\cos \alpha ,\cos \beta ,\cos \gamma ) r = ∣ r ∣ ( cos α , cos β , cos γ )