一元函数积分学 不定积分 原函数与不定积分的概念及性质 积分是求导的逆运算 ,不定积分的本质就是已知导数(微分)求原函数的过程。
原函数F ′ ( x ) = f ( x ) F'(x)=f(x) F ′ ( x ) = f ( x ) d F ( x ) = f ( x ) d x dF(x)=f(x)dx d F ( x ) = f ( x ) d x F ( x ) F(x) F ( x ) f ( x ) f(x) f ( x ) 一个原函数 。原函数存在定理 :如果函数在某区间内连续 ,则其在该区间内必有原函数;原函数性质 :如果函数f ( x ) f(x) f ( x ) F ( x ) F(x) F ( x ) f ( x ) f(x) f ( x ) F ( x ) + C F(x)+C{\color{Red} } F ( x ) + C C C C
不定积分f ( x ) f(x) f ( x ) f ( x ) f(x) f ( x ) 不定积分 ,记为∫ f ( x ) d x \int f(x)dx ∫ f ( x ) d x ∫ \int ∫ f ( x ) f(x) f ( x ) f ( x ) d x f(x)dx f ( x ) d x x x x f ( x ) f(x) f ( x ) f ( x ) f(x) f ( x ) ∫ f ( x ) d x = F ( x ) + C \int f(x)dx=F(x)+C ∫ f ( x ) d x = F ( x ) + C ∫ x 3 d x \int x^3dx ∫ x 3 d x = x 4 4 + C =\frac{x^4}{4}+C = 4 x 4 + C ∫ e x d x \int e^xdx ∫ e x d x e x + C e^x+C e x + C ∫ 1 1 + x 2 d x \int \frac{1}{1+x^2}dx ∫ 1 + x 2 1 d x arctan x + C \arctan x +C arctan x + C ∫ 1 x d x \int \frac{1}{x}dx ∫ x 1 d x ln ∣ x ∣ + C \ln|x|+C{\color{Orange} } ln ∣ x ∣ + C
基本积分公式 :∫ k d x = k x + C \int kdx=kx+C ∫ k d x = k x + C ∫ x μ d x = x μ + 1 μ + 1 + C \int x^\mu dx=\frac{x^{\mu +1} }{\mu +1} +C ∫ x μ d x = μ + 1 x μ + 1 + C ∫ 1 x d x = ln ∣ x ∣ + C \int \frac{1}{x} dx=\ln |x|+C ∫ x 1 d x = ln ∣ x ∣ + C ∫ e x d x = e x + C \int e^x dx=e^x+C ∫ e x d x = e x + C ∫ 1 1 + x 2 d x = arctan x + C \int \frac{1}{1+x^2} dx=\arctan x+C ∫ 1 + x 2 1 d x = arctan x + C ∫ 1 1 − x 2 d x = arcsin x + C \int \frac{1}{\sqrt{1-x^2} } dx=\arcsin x+C ∫ 1 − x 2 1 d x = arcsin x + C ∫ cos x d x = sin x + C \int \cos x dx=\sin x+C ∫ cos x d x = sin x + C ∫ sin x d x = − cos x + C \int \sin x dx=-\cos x+C ∫ sin x d x = − cos x + C ∫ 1 cos 2 x d x = ∫ sec 2 x d x = tan x + C \int \frac{1}{\cos^2x} dx=\int \sec^2 xdx=\tan x+C ∫ c o s 2 x 1 d x = ∫ sec 2 x d x = tan x + C ∫ 1 sin 2 x d x = ∫ csc 2 x d x = − cot x + C \int \frac{1}{\sin^2x} dx=\int \csc^2 xdx=-\cot x+C ∫ s i n 2 x 1 d x = ∫ csc 2 x d x = − cot x + C ∫ sec x tan x d x = sec x + C \int \sec x \tan x dx=\sec x+C ∫ sec x tan x d x = sec x + C ∫ csc x cot x d x = − cot x + C \int \csc x \cot x dx=-\cot x+C ∫ csc x cot x d x = − cot x + C 不定积分的性质f ( x ) f(x) f ( x ) g ( x ) g(x) g ( x ) ∫ [ f ( x ) ± g ( x ) ] d x = ∫ f ( x ) d x ± ∫ g ( x ) d x \int [f(x) \pm g(x)]dx=\int f(x)dx \pm \int g(x)dx ∫ [ f ( x ) ± g ( x ) ] d x = ∫ f ( x ) d x ± ∫ g ( x ) d x f ( x ) f(x) f ( x ) k k k ∫ k f ( x ) d x = k ∫ f ( x ) d x \int kf(x)dx=k \int f(x)dx ∫ k f ( x ) d x = k ∫ f ( x ) d x f ( x ) f(x) f ( x ) [ ∫ f ( x ) d x ] ′ = f ( x ) ; d [ ∫ f ( x ) d x ] = f ( x ) d x [\int f(x)dx]'=f(x);d[\int f(x)dx]=f(x)dx [ ∫ f ( x ) d x ] ′ = f ( x ) ; d [ ∫ f ( x ) d x ] = f ( x ) d x f ( x ) f(x) f ( x ) ∫ f ′ ( x ) d x = f ( x ) + C ; ∫ d f ( x ) = f ( x ) + C \int f'(x)dx=f(x)+C;\int df(x)=f(x)+C ∫ f ′ ( x ) d x = f ( x ) + C ; ∫ d f ( x ) = f ( x ) + C 规律1 :先积后导=本身;先积后微=本身d x dx d x C C C 规律2 :最外层是d d d d x dx d x ∫ \int ∫ C C C ′ ' ′ d x dx d x C C C f ( x ) f(x) f ( x ) ∫ f ′ ( x ) d x = f ( x ) \int f'(x)dx=f(x) ∫ f ′ ( x ) d x = f ( x ) d [ ∫ f ( x ) d x ] = f ( x ) d[\int f(x) dx]=f(x) d [ ∫ f ( x ) d x ] = f ( x ) [ ∫ f ( x ) d x ] ′ = f ( x ) + C [\int f(x) dx]'=f(x)+C [ ∫ f ( x ) d x ] ′ = f ( x ) + C d d x [ ∫ f ( x ) d x ] = f ( x ) \frac{d}{dx} [\int f(x) dx]=f(x) d x d [ ∫ f ( x ) d x ] = f ( x ) ∫ \int ∫ C C C d x dx d x d x dx d x e − x e^{-x} e − x f ( x ) f(x) f ( x ) ∫ f ′ ( x ) d x = e − x \int f'(x)dx=e^{-x} ∫ f ′ ( x ) d x = e − x ∫ f ( x ) d x = e − x \int f(x)dx=e^{-x} ∫ f ( x ) d x = e − x d [ ∫ f ′ ( x ) d x ] ′ = e − x d x d[\int f'(x) dx]'=e^{-x}dx d [ ∫ f ′ ( x ) d x ] ′ = e − x d x d [ ∫ f ( x ) d x ] = − e − x d x d [\int f(x) dx]=-e^{-x}dx d [ ∫ f ( x ) d x ] = − e − x d x ∫ \int ∫ C C C f ( x ) f(x) f ( x ) cos x \cos x cos x f ′ ( x ) = f'(x)= f ′ ( x ) = sin x \sin x sin x − sin x -\sin x − sin x − cos x -\cos x − cos x cos x \cos x cos x cos x → − sin x → − cos x \cos x \to -\sin x \to -\cos x cos x → − sin x → − cos x F ( x ) F(x) F ( x ) ln cos x \ln \cos x ln cos x d F ( x ) = dF(x)= d F ( x ) = ln cos x d x \ln \cos x dx{\color{Red} } ln cos x d x f ( x ) f(x) f ( x ) d [ ∫ f ( 2 x ) d x ] = d[\int f(2x)dx]= d [ ∫ f ( 2 x ) d x ] = f ( 2 x ) f(2x) f ( 2 x ) f ( 2 x ) + C f(2x)+C f ( 2 x ) + C f ( 2 x ) d x f(2x)dx f ( 2 x ) d x f ′ ( 2 x ) d x f'(2x)dx f ′ ( 2 x ) d x d d d d x dx d x
直接积分法 根据基本积分公式以及第一第二基本性质;∫ ( e x − 3 cos x ) d x \int (e^x-3\cos x)dx ∫ ( e x − 3 cos x ) d x = ∫ e x d x − 3 ∫ cos x d x =\int e^xdx-3\int \cos x dx = ∫ e x d x − 3 ∫ cos x d x = e x − 3 sin x + C =e^x-3\sin x+C = e x − 3 sin x + C ∫ x ( x 2 − 5 ) d x \int \sqrt{x}(x^2-5)dx ∫ x ( x 2 − 5 ) d x = ∫ ( x 5 2 − 5 x 1 2 ) d x =\int (x^{\frac{5}{2}}-5x^{\frac{1}{2} })dx = ∫ ( x 2 5 − 5 x 2 1 ) d x ∫ x 5 2 d x − 5 ∫ x 1 2 \int x^{\frac{5}{2} }dx-5\int x^{\frac{1}{2} } ∫ x 2 5 d x − 5 ∫ x 2 1 = 2 7 x 7 2 − 10 3 x 3 2 + C =\frac{2}{7}x^{\frac{7}{2} }-\frac{10}{3}x^{\frac{3}{2} }+C = 7 2 x 2 7 − 3 1 0 x 2 3 + C = 2 7 x 7 2 − 10 3 x + C =\frac{2}{7}x^{\frac{7}{2} }-\frac{10}{3}\sqrt{x}+C = 7 2 x 2 7 − 3 1 0 x + C ∫ d x x 3 \int \frac{dx}{x^3} ∫ x 3 d x = ∫ 1 x 3 d x =\int \frac{1}{x^{3} }dx = ∫ x 3 1 d x = − x − 2 2 + C =-\frac{x-2}{2}+C = − 2 x − 2 + C = − 1 2 x 2 + C =-\frac{1}{2x^2}+C = − 2 x 2 1 + C ∫ d x x 3 x 3 d x \int \frac{dx}{x^3\sqrt[3]{x} }dx ∫ x 3 3 x d x d x = ∫ x − 4 3 d x =\int x^{-\frac{4}{3} }dx = ∫ x − 3 4 d x = x − 1 3 − 1 3 + C =\frac{x^{-\frac{1}{3} } }{-\frac{1}{3} }+C = − 3 1 x − 3 1 + C = − 3 x 3 + C =-\frac{3}{\sqrt[3]{x} }+C = − 3 x 3 + C ∫ ( 2 1 + x 2 − 1 2 1 − x 2 + 3 x ) d x \int (\frac{2}{1+x^2}-\frac{1}{2\sqrt{1-x^2} }+\frac{3}{x} )dx ∫ ( 1 + x 2 2 − 2 1 − x 2 1 + x 3 ) d x = 2 ∫ 1 1 + x 2 d x − 1 2 ∫ 1 1 − x 2 d x + 3 ∫ 1 x d x =2\int \frac{1}{1+x^2}dx-\frac{1}{2}\int \frac{1}{\sqrt{1-x^2} }dx+3\int \frac{1}{x}dx = 2 ∫ 1 + x 2 1 d x − 2 1 ∫ 1 − x 2 1 d x + 3 ∫ x 1 d x = 2 arctan x − 1 2 arcsin x + 3 ln ∣ x ∣ + C =2\arctan x-\frac{1}{2} \arcsin x+3\ln |x|+C = 2 arctan x − 2 1 arcsin x + 3 ln ∣ x ∣ + C ∫ ( x − x 3 ) 2 d x \int (\sqrt{x}-\sqrt[3]{x} )^2dx ∫ ( x − 3 x ) 2 d x = ∫ ( ( x ) 2 + ( x 3 ) 2 − 2 x ⋅ x 3 ) d x =\int ((\sqrt{x} )^2+(\sqrt[3]{x})^2-2\sqrt{x} \cdot \sqrt[3]{x} )dx = ∫ ( ( x ) 2 + ( 3 x ) 2 − 2 x ⋅ 3 x ) d x = ∫ ( x + x 2 3 − 2 x 5 6 d x =\int (x +x^{\frac{2}{3} } -2x^{\frac{5}{6} }dx = ∫ ( x + x 3 2 − 2 x 6 5 d x = 1 2 x 2 + x 5 3 5 3 − 2 x 11 6 11 6 + C =\frac{1}{2}x^2+\frac{x^{\frac{5}{3} } }{\frac{5}{3} }-2\frac{x^{\frac{11}{6} } }{\frac{11}{6} }+C = 2 1 x 2 + 3 5 x 3 5 − 2 6 1 1 x 6 1 1 + C = 1 2 x 2 + 3 5 x 5 3 − 12 11 x 11 6 + C =\frac{1}{2}x^2+\frac{3}{5}x^{\frac{5}{3} }-\frac{12}{11}x^{\frac{11}{6} }+C = 2 1 x 2 + 5 3 x 3 5 − 1 1 1 2 x 6 1 1 + C ∫ ( x − 1 ) 3 x 2 d x \int \frac{(x-1)^3}{x^2}dx ∫ x 2 ( x − 1 ) 3 d x = ∫ x 3 − 3 x 2 + 3 x − 1 x 2 d x =\int \frac{x^3-3x^2+3x-1}{x^2}dx = ∫ x 2 x 3 − 3 x 2 + 3 x − 1 d x = ∫ ( x − 3 + 3 x − 1 x 2 ) d x =\int (x-3+\frac{3}{x}-\frac{1}{x^2} )dx = ∫ ( x − 3 + x 3 − x 2 1 ) d x = 1 2 x 2 − 3 x + 3 ln ∣ x ∣ + 1 x + C =\frac{1}{2}x^2-3x+3\ln |x|+\frac{1}{x}+C = 2 1 x 2 − 3 x + 3 ln ∣ x ∣ + x 1 + C ∫ 2 + 3 x 2 1 + x 2 d x \int \frac{2+3x^2}{1+x^2}dx ∫ 1 + x 2 2 + 3 x 2 d x = ∫ 3 + 3 x 2 − 1 1 + x 2 d x =\int \frac{3+3x^2-1}{1+x^2}dx = ∫ 1 + x 2 3 + 3 x 2 − 1 d x = ∫ ( 3 + 1 1 + x 2 ) d x =\int (3+\frac{1}{1+x^2} )dx = ∫ ( 3 + 1 + x 2 1 ) d x = 3 x − arctan x + C =3x-\arctan x+C = 3 x − arctan x + C ∫ 1 x 2 − 5 x + 6 d x \int \frac{1}{x^2-5x+6}dx ∫ x 2 − 5 x + 6 1 d x = ∫ 1 ( x − 3 ) ( x − 2 ) d x =\int \frac{1}{(x-3)(x-2)}dx = ∫ ( x − 3 ) ( x − 2 ) 1 d x 1 ( x − 2 ) ( z − 3 ) ⟶ a x − 2 − b x − 3 {\color{Violet} \frac{1}{(x-2)(z-3)} \longrightarrow \frac{a}{x-2}-\frac{b}{x-3 } } ( x − 2 ) ( z − 3 ) 1 ⟶ x − 2 a − x − 3 b a , b a,b a , b a = b = − 1 a=b=-1 a = b = − 1 = ∫ ( 1 x − 3 − 1 x − 2 ) d x =\int (\frac{1}{x-3}-\frac{1}{x-2} )dx = ∫ ( x − 3 1 − x − 2 1 ) d x = ln ∣ x − 3 ∣ − ln ∣ x − 2 ∣ + C =\ln |x-3|-\ln |x-2|+C = ln ∣ x − 3 ∣ − ln ∣ x − 2 ∣ + C = ln ∣ x − 3 x − 2 ∣ + C =\ln |\frac{x-3}{x-2} |+C = ln ∣ x − 2 x − 3 ∣ + C ∫ cos 2 x cos 2 x sin 2 x d x \int \frac{\cos 2x}{\cos^2x \sin^2x}dx ∫ c o s 2 x s i n 2 x c o s 2 x d x cos 2 x = cos 2 x − sin 2 x = 2 cos 2 x − 1 = 1 − 2 sin 2 x {\color{Red} \cos 2x=\cos^2x-\sin^2x}=2\cos^2x-1=1-2\sin^2x c o s 2 x = c o s 2 x − s i n 2 x = 2 cos 2 x − 1 = 1 − 2 sin 2 x ∫ 1 cos 2 x d x = ∫ sec 2 x d x = tan x + C {\color{Blue} \int \frac{1}{\cos^2x}dx=\int \sec^2xdx=\tan x+C } ∫ c o s 2 x 1 d x = ∫ s e c 2 x d x = t a n x + C ∫ 1 sin 2 x d x = ∫ csc 2 x d x = − cot x + C {\color{Blue} \int \frac{1}{\sin^2x}dx=\int \csc^2xdx=-\cot x+C } ∫ s i n 2 x 1 d x = ∫ c s c 2 x d x = − c o t x + C = ∫ ( 1 sin 2 x − 1 cos 2 x ) d x =\int (\frac{1}{\sin^2x}-\frac{1}{\cos^2x} )dx = ∫ ( s i n 2 x 1 − c o s 2 x 1 ) d x = ∫ cos 2 x − sin 2 x cos 2 x sin 2 x d x =\int \frac{\cos^2x-\sin^2x}{\cos^2x \sin^2x}dx = ∫ c o s 2 x s i n 2 x c o s 2 x − s i n 2 x d x = ∫ ( 1 sin 2 x − 1 cos 2 x ) d x =\int (\frac{1}{\sin^2x}-\frac{1}{\cos^2x} )dx = ∫ ( s i n 2 x 1 − c o s 2 x 1 ) d x = − cot x − tan x + C =-\cot x-\tan x+C = − cot x − tan x + C ∫ sin 2 x 2 d x \int \sin^2\frac{x}{2}dx ∫ sin 2 2 x d x cos 2 x = 1 − 2 sin 2 x \cos 2x=1-2\sin^2x cos 2 x = 1 − 2 sin 2 x x = x 2 x=\frac{x}{2} x = 2 x cos x = 1 − 2 sin 2 x 2 \cos x=1-2\sin^2\frac{x}{2} cos x = 1 − 2 sin 2 2 x sin 2 x 2 = 1 − cos x 2 \sin^2\frac{x}{2}=\frac{1-\cos x}{2} sin 2 2 x = 2 1 − c o s x = ∫ ( 1 2 − 1 2 cos x ) d x =\int (\frac{1}{2}-\frac{1}{2}\cos x)dx = ∫ ( 2 1 − 2 1 cos x ) d x = 1 2 x − 1 2 sin x + C =\frac{1}{2}x-\frac{1}{2}\sin x+C = 2 1 x − 2 1 sin x + C ∫ tan 2 x d x \int \tan^2xdx ∫ tan 2 x d x tan 2 x = sec 2 x − 1 \tan^2x=\sec^2x-1 tan 2 x = sec 2 x − 1 ∫ sec 2 x d x = tan x + C \int \sec^2xdx=\tan x+C ∫ sec 2 x d x = tan x + C = ∫ ( sec 2 x − 1 ) d x = tan x − x + C =\int (\sec^2x-1)dx=\tan x-x+C = ∫ ( sec 2 x − 1 ) d x = tan x − x + C 基本代数式,可做恒等变形 :( a + b ) 2 = a 2 + 2 a b + b 2 {\color{Red} (a+b)^2=a^2+2ab+b^2} ( a + b ) 2 = a 2 + 2 a b + b 2 ( a − b ) 2 = a 2 − 2 a b + b 2 {\color{Red} (a-b)^2=a^2-2ab+b^2} ( a − b ) 2 = a 2 − 2 a b + b 2 ( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 {\color{Red} (a+b)^3=a^3+3a^2b+3ab^2+b^3} ( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 ( a − b ) 3 = a 3 − 3 a 2 b + 3 a b 2 − b 3 {\color{Red} (a-b)^3=a^3-3a^2b+3ab^2-b^3} ( a − b ) 3 = a 3 − 3 a 2 b + 3 a b 2 − b 3 a 2 − b 2 = ( a + b ) ( a − b ) {\color{Red} a^2-b^2=(a+b)(a-b)} a 2 − b 2 = ( a + b ) ( a − b ) a 3 − b 3 = ( a − b ) ( a 2 + a b + b 2 ) {\color{Red} a^3-b^3=(a-b)(a^2+ab+b^2)} a 3 − b 3 = ( a − b ) ( a 2 + a b + b 2 ) a 3 + b 3 = ( a + b ) ( a 2 − a b + b 2 ) {\color{Red} a^3+b^3=(a+b)(a^2-ab+b^2)} a 3 + b 3 = ( a + b ) ( a 2 − a b + b 2 ) cos 2 x = cos 2 x − sin 2 x = 2 cos 2 x − 1 = 1 − 2 sin 2 x {\color{Purple} \cos 2x=\cos^2x-\sin^2x=2\cos^2x-1=1-2\sin^2x} c o s 2 x = c o s 2 x − s i n 2 x = 2 c o s 2 x − 1 = 1 − 2 s i n 2 x sin 2 x = 2 sin x cos x {\color{Purple} \sin 2x=2\sin x \cos x} s i n 2 x = 2 s i n x c o s x sin x 2 + cos x 2 = 1 {\color{Purple} \sin x^2+\cos x^2 =1} s i n x 2 + c o s x 2 = 1 tan x 2 + 1 = sec x 2 {\color{Purple} \tan x^2+1=\sec x^2} t a n x 2 + 1 = s e c x 2 1 − cot x 2 = csc x 2 {\color{Purple} 1-\cot x^2=\csc x^2} 1 − c o t x 2 = c s c x 2
第一类换元法(凑微分法) 积分式较为复杂,不能直接套用基本积分公式,整体结构为∫ u ′ f ( u ) d x \int u'f(u)dx ∫ u ′ f ( u ) d x u ′ f ( u ) d x u'f(u)dx u ′ f ( u ) d x d u du d u ∫ f ( u ) d u \int f(u)du ∫ f ( u ) d u ∫ cos 2 x sin x d x \int \cos^2x\sin xdx ∫ cos 2 x sin x d x = − ∫ cos 2 x ⋅ ( − sin x ) d x =-\int \cos^2x \cdot (-\sin x)dx = − ∫ cos 2 x ⋅ ( − sin x ) d x = − ∫ cos 2 x d sin x =-\int \cos^2xd\sin x = − ∫ cos 2 x d sin x = − 1 3 cos 3 x + C =-\frac{1}{3}\cos^3x+C = − 3 1 cos 3 x + C ∫ 2 cos 2 x d x \int 2\cos 2xdx ∫ 2 cos 2 x d x = ∫ cos 2 x ⋅ 2 d x =\int \cos 2x \cdot 2dx = ∫ cos 2 x ⋅ 2 d x = ∫ cos 2 x d 2 x =\int \cos 2xd 2x = ∫ cos 2 x d 2 x = sin 2 x + C =\sin 2x+C = sin 2 x + C ∫ 2 x e x 2 d x \int 2xe^{x^2}dx ∫ 2 x e x 2 d x = ∫ e x 2 ⋅ 2 x d x =\int e^{x^2}\cdot 2xdx = ∫ e x 2 ⋅ 2 x d x = e x 2 d x 2 =e^{x^2}dx^2 = e x 2 d x 2 = e x 2 + C =e^{x^2}+C = e x 2 + C ∫ 1 2 x + 3 d x \int \frac{1}{2x+3}dx ∫ 2 x + 3 1 d x = 1 2 ∫ 1 2 x + 3 2 d x =\frac{1}{2}\int \frac{1}{2x+3}2dx = 2 1 ∫ 2 x + 3 1 2 d x = 1 2 ∫ 1 2 x + 3 2 d x d ( 2 x + 3 ) =\frac{1}{2}\int \frac{1}{2x+3}2dxd(2x+3) = 2 1 ∫ 2 x + 3 1 2 d x d ( 2 x + 3 ) = 1 2 ln ∣ 2 x + 3 ∣ + C =\frac{1}{2}\ln |2x+3|+C = 2 1 ln ∣ 2 x + 3 ∣ + C 总结公式 :∫ 1 a x + b d x = 1 a l n ∣ a x + b ∣ + C ( a ≠ 0 ) {\color{Red} \int \frac{1}{ax+b}dx=\frac{1}{a}ln|ax+b|+C (a \ne 0) } ∫ a x + b 1 d x = a 1 l n ∣ a x + b ∣ + C ( a = 0 ) ∫ 1 4 + x 2 d x \int \frac{1}{4+x^2}dx ∫ 4 + x 2 1 d x ∫ 1 1 + x 2 d x = arctan x + C ⟹ ∫ 1 1 + □ 2 d □ = arctan □ + C \int \frac{1}{1+x^2}dx=\arctan x+C\Longrightarrow \int \frac{1}{1+\Box ^2} d\Box =\arctan \Box +C ∫ 1 + x 2 1 d x = arctan x + C ⟹ ∫ 1 + □ 2 1 d □ = arctan □ + C = 1 4 ⋅ 1 1 + ( x 2 ) 2 d x =\frac{1}{4}\cdot \frac{1}{1+(\frac{x}{2})^2}dx = 4 1 ⋅ 1 + ( 2 x ) 2 1 d x = 1 2 ∫ 1 1 + ( x 2 ) 2 ⋅ 1 2 d x =\frac{1}{2} \int \frac{1}{1+(\frac{x}{2})^2}\cdot \frac{1}{2}dx = 2 1 ∫ 1 + ( 2 x ) 2 1 ⋅ 2 1 d x = 1 2 ∫ 1 1 + x 2 d x 2 =\frac{1}{2} \int \frac{1}{1+x^2}d\frac{x}{2} = 2 1 ∫ 1 + x 2 1 d 2 x = 1 2 arctan x + C =\frac{1}{2} \arctan x+C = 2 1 arctan x + C 总结公式 :∫ 1 a 2 + x 2 d x = 1 a arctan x a + C ( a ≠ 0 ) {\color{Red} \int \frac{1}{a^2+x^2}dx=\frac{1}{a}\arctan \frac{x}{a}+C (a \ne 0) } ∫ a 2 + x 2 1 d x = a 1 a r c t a n a x + C ( a = 0 ) ∫ 1 x 2 − 1 d x \int \frac{1}{x^2-1}dx ∫ x 2 − 1 1 d x = 1 2 ∫ ( 1 ( x − 1 ) − 1 x + 1 ) d x =\frac{1}{2}\int (\frac{1}{(x-1)}-\frac{1}{x+1})dx = 2 1 ∫ ( ( x − 1 ) 1 − x + 1 1 ) d x = ∫ ( 1 2 ( x − 1 ) − 1 2 ( x + 1 ) ) d x =\int (\frac{1}{2(x-1)}-\frac{1}{2(x+1)} )dx = ∫ ( 2 ( x − 1 ) 1 − 2 ( x + 1 ) 1 ) d x = 1 2 ∫ 1 x − 1 − 1 2 d x ∫ 1 x + 1 d x =\frac{1}{2}\int \frac{1}{x-1}-\frac{1}{2}dx \int \frac{1}{x+1}dx = 2 1 ∫ x − 1 1 − 2 1 d x ∫ x + 1 1 d x = 1 2 ∫ 1 x − 1 d ( x − 1 ) − 1 2 ∫ 1 x + 1 d ( x + 1 ) =\frac{1}{2}\int \frac{1}{x-1}d(x-1)-\frac{1}{2}\int \frac{1}{x+1}d(x+1) = 2 1 ∫ x − 1 1 d ( x − 1 ) − 2 1 ∫ x + 1 1 d ( x + 1 ) = 1 2 ln ∣ x − 1 ∣ − 1 2 ln ∣ x + 1 ∣ + C =\frac{1}{2}\ln |x-1|-\frac{1}{2}\ln |x+1|+C = 2 1 ln ∣ x − 1 ∣ − 2 1 ln ∣ x + 1 ∣ + C = 1 2 ln ∣ x − 1 x + 1 ∣ + C =\frac{1}{2}\ln |\frac{x-1}{x+1} |+C = 2 1 ln ∣ x + 1 x − 1 ∣ + C 总结公式 :∫ 1 x 2 − a 2 d x = 1 2 a ln ∣ x − a x + a ∣ + C ( a ≠ 0 ) {\color{Red} \int \frac{1}{x^2-a^2}dx=\frac{1}{2a}\ln |\frac{x-a}{x+a}|+C (a \ne 0) } ∫ x 2 − a 2 1 d x = 2 a 1 l n ∣ x + a x − a ∣ + C ( a = 0 ) ∫ 1 4 − x 2 d x \int \frac{1}{\sqrt{4-x^2} }dx ∫ 4 − x 2 1 d x ∫ 1 ( 1 − x 2 ) d x = arcsin x + C ⟹ ∫ 1 1 − □ 2 d □ = arcsin □ + C \int \frac{1}{\sqrt(1-x^2)}dx=\arcsin x+C\Longrightarrow \int \frac{1}{1-\Box ^2} d\Box =\arcsin \Box +C ∫ ( 1 − x 2 ) 1 d x = arcsin x + C ⟹ ∫ 1 − □ 2 1 d □ = arcsin □ + C = ∫ 1 4 − x 2 d x =\int \frac{1}{\sqrt{4-x^2} }dx = ∫ 4 − x 2 1 d x = ∫ 1 1 − x 2 4 ⋅ 4 d x =\int \frac{1}{\sqrt{1-\frac{x^2}{4}\cdot 4} } dx = ∫ 1 − 4 x 2 ⋅ 4 1 d x = ∫ 1 2 ⋅ 1 − ( x 2 ) 2 d x =\int \frac{1}{2\cdot \sqrt{1-(\frac{x}{2})^2} }dx = ∫ 2 ⋅ 1 − ( 2 x ) 2 1 d x = ∫ 1 1 − ( x 2 ) 2 ⋅ 1 2 d x =\int \frac{1}{\sqrt{1-(\frac{x}{2})^2} }\cdot \frac{1}{2}dx = ∫ 1 − ( 2 x ) 2 1 ⋅ 2 1 d x = ∫ 1 1 − ( x 2 ) 2 d ( x 2 ) =\int \frac{1}{\sqrt{1-(\frac{x}{2})^2} }d(\frac{x}{2}) = ∫ 1 − ( 2 x ) 2 1 d ( 2 x ) = arcsin x 2 + C =\arcsin \frac{x}{2}+C = arcsin 2 x + C 总结公式 :∫ 1 a 2 − x 2 d x = arcsin x a ∣ + C ( a > 0 ) {\color{Red} \int \frac{1}{\sqrt{a^2-x^2} }dx=\arcsin \frac{x}{a}|+C (a > 0) } ∫ a 2 − x 2 1 d x = a r c s i n a x ∣ + C ( a > 0 ) ∫ e x x d x \int \frac{e^{\sqrt{x} } }{\sqrt{x} }dx ∫ x e x d x = ∫ e x ⋅ 1 x ⋅ 1 2 ⋅ 2 d x =\int e^{\sqrt{x} } \cdot \frac{1}{\sqrt{x} }\cdot \frac{1}{2} \cdot 2dx = ∫ e x ⋅ x 1 ⋅ 2 1 ⋅ 2 d x = 2 ∫ e 2 x d x =2\int e^{2\sqrt{x} }dx = 2 ∫ e 2 x d x = 2 ∫ e x d x =2\int e^{\sqrt{x} }d\sqrt{x} = 2 ∫ e x d x = 2 e x + C =2e^{\sqrt{x} }+C = 2 e x + C ∫ tan x d x \int \tan xdx ∫ tan x d x = ∫ sin x cos x d x =\int \frac{\sin x}{\cos x}dx = ∫ c o s x s i n x d x = − ∫ 1 cos x d cos x =-\int \frac{1}{\cos x}d\cos x = − ∫ c o s x 1 d cos x = − ln ∣ cos x ∣ + C =-\ln |\cos x|+C = − ln ∣ cos x ∣ + C 总结公式 :∫ tan x d x = − ln ∣ cos x ∣ + C {\color{Red} \int \tan xdx=-\ln | \cos x|+C } ∫ t a n x d x = − l n ∣ c o s x ∣ + C ∫ sec x d x \int \sec xdx ∫ sec x d x ∫ 1 cos 2 x d x = ∫ sec 2 x d x = tan x + C \int \frac{1}{\cos^2x}dx=\int \sec^2xdx=\tan x+C ∫ c o s 2 x 1 d x = ∫ sec 2 x d x = tan x + C ∫ sec x tan x d x = sec x + C \int \sec x\tan xdx=\sec x+C ∫ sec x tan x d x = sec x + C = ∫ sec x ⋅ ( sec x + tan x ) sec x + tan x d x =\int \frac{\sec x \cdot (\sec x+\tan x)}{\sec x+\tan x}dx = ∫ s e c x + t a n x s e c x ⋅ ( s e c x + t a n x ) d x = ∫ sec 2 x + sec x ⋅ tan x ) sec x + tan x d x =\int \frac{\sec^2x+\sec x\cdot \tan x)}{\sec x+\tan x}dx = ∫ s e c x + t a n x s e c 2 x + s e c x ⋅ t a n x ) d x = ∫ 1 sec x + tan x d ( sec x + tan x ) =\int \frac{1}{\sec x+\tan x}d(\sec x+\tan x) = ∫ s e c x + t a n x 1 d ( sec x + tan x ) = ln ∣ sec x + tan x ∣ + C =\ln |\sec x+\tan x|+C = ln ∣ sec x + tan x ∣ + C 总结公式 :∫ sec x d x = ln ∣ sec x + tan x ∣ + C {\color{Red} \int \sec xdx=\ln |\sec x+\tan x|+C } ∫ s e c x d x = l n ∣ s e c x + t a n x ∣ + C ∫ sin 3 x d x \int \sin^3xdx ∫ sin 3 x d x = ∫ sin x ⋅ sin 2 x d x =\int \sin x\cdot \sin^2xdx = ∫ sin x ⋅ sin 2 x d x = ∫ ( 1 − cos 2 x ) ⋅ ( − sin x ) d x =\int (1-\cos^2x)\cdot (-\sin x)dx = ∫ ( 1 − cos 2 x ) ⋅ ( − sin x ) d x = ∫ ( cos 2 x − 1 ) d ( cos x ) =\int (\cos^2x-1)d(\cos x) = ∫ ( cos 2 x − 1 ) d ( cos x ) = ∫ cos 2 x d ( cos x ) − ∫ 1 d ( cos x ) =\int \cos^2xd(\cos x)-\int 1d(\cos x) = ∫ cos 2 x d ( cos x ) − ∫ 1 d ( cos x ) = 1 3 cos 3 x − cos x + C =\frac{1}{3}\cos^3x-\cos x+C = 3 1 cos 3 x − cos x + C ∫ x 2 ( x + 1 ) 3 d x \int \frac{x^2}{(x+1)^3}dx ∫ ( x + 1 ) 3 x 2 d x x + 1 = t , x = t − 1 , d x = d ( t − 1 ) = d t x+1=t,x=t-1,dx=d(t-1)=dt x + 1 = t , x = t − 1 , d x = d ( t − 1 ) = d t = ∫ ( t − 1 ) 2 t 3 d t =\int \frac{(t-1)^2}{t^3}dt = ∫ t 3 ( t − 1 ) 2 d t = ∫ t 2 − 2 t + 1 t 3 d t =\int \frac{t^2-2t+1}{t^3}dt = ∫ t 3 t 2 − 2 t + 1 d t = ∫ ( 1 t − 2 t 2 + 1 t 3 ) d t =\int (\frac{1}{t}-\frac{2}{t^2}+\frac{1}{t^3} )dt = ∫ ( t 1 − t 2 2 + t 3 1 ) d t = ln ∣ t ∣ + 2 t − 1 2 t 2 + C =\ln |t|+\frac{2}{t}-\frac{1}{2t^2}+C = ln ∣ t ∣ + t 2 − 2 t 2 1 + C = ln ∣ x + 1 ∣ + 2 x + 1 − 1 2 ( x + 1 ) 2 + C =\ln |x+1|+\frac{2}{x+1}-\frac{1}{2(x+1)^2}+C = ln ∣ x + 1 ∣ + x + 1 2 − 2 ( x + 1 ) 2 1 + C ∫ ( x + 2 ) 3 ( x + 3 ) d x \int \frac{(x+2)^3}{(x+3)}dx ∫ ( x + 3 ) ( x + 2 ) 3 d x x + 3 = t , x = t − 3 , d x = d ( t − 3 ) = d t x+3=t,x=t-3,dx=d(t-3)=dt x + 3 = t , x = t − 3 , d x = d ( t − 3 ) = d t = ∫ ( t − 1 ) 3 t d t = \int \frac{(t-1)^3}{t}dt = ∫ t ( t − 1 ) 3 d t = ∫ ( t 3 − 3 t 2 + 3 t − 1 t 2 ) d t =\int (\frac{t^3-3t^2+3t-1}{t^2} )dt = ∫ ( t 2 t 3 − 3 t 2 + 3 t − 1 ) d t = ∫ ( t − 3 + 3 t − 1 t 2 ) d t =\int (t-3+\frac{3}{t}-\frac{1}{t^2} )dt = ∫ ( t − 3 + t 3 − t 2 1 ) d t = t 2 2 − 3 t + 3 ln ∣ t ∣ + 1 t + C =\frac{t^2}{2}-3t+3\ln |t|+\frac{1}{t}+C = 2 t 2 − 3 t + 3 ln ∣ t ∣ + t 1 + C = 1 2 ( x + 3 ) 2 − 3 ( x + 3 ) + 3 ln ∣ x + 3 ∣ + 1 x + 3 + C =\frac{1}{2}(x+3)^2-3(x+3)+3\ln |x+3|+\frac{1}{x+3}+C = 2 1 ( x + 3 ) 2 − 3 ( x + 3 ) + 3 ln ∣ x + 3 ∣ + x + 3 1 + C
第二类换元法(根式代换法) 例题1:求∫ 1 1 + 2 x + 3 d x \int \frac{1}{1+\sqrt{2x+3} }dx ∫ 1 + 2 x + 3 1 d x 2 x + 3 = t 2 , x = t 2 − 3 2 , d x = t d t 2x+3=t^2,x=\frac{t^2-3}{2},dx=tdt 2 x + 3 = t 2 , x = 2 t 2 − 3 , d x = t d t = ∫ 1 1 + t t d t = \int \frac{1}{1+t}tdt = ∫ 1 + t 1 t d t = ∫ t + 1 − 1 1 + t d t =\int \frac{t+1-1}{1+t}dt = ∫ 1 + t t + 1 − 1 d t = ( 1 − 1 1 + t ) =(1-\frac{1}{1+t}) = ( 1 − 1 + t 1 ) = t − ln ∣ 1 + t ∣ + C =t-\ln|1+t|+C = t − ln ∣ 1 + t ∣ + C = 2 x + 3 − ln ∣ 2 x + 3 + 1 ∣ + C =\sqrt{2x+3}-\ln |\sqrt{2x+3}+1|+C = 2 x + 3 − ln ∣ 2 x + 3 + 1 ∣ + C a x + b n \sqrt[n]{ax+b} n a x + b ∫ 2 x + x 3 d x \int \frac{2}{x+\sqrt[3]{x} }dx ∫ x + 3 x 2 d x x = t 3 , x 1 3 = t , d x = 3 t 2 d t x=t^3,x^{\frac{1}{3} }=t,dx=3t^2dt x = t 3 , x 3 1 = t , d x = 3 t 2 d t = ∫ 2 t 3 + t 3 t 2 d t =\int \frac{2}{t^3+t}3t^2dt = ∫ t 3 + t 2 3 t 2 d t = ∫ 6 t t 2 + 1 d t =\int \frac{6t}{t^2+1}dt = ∫ t 2 + 1 6 t d t = 3 ∫ 1 t 2 + 1 d ( t 2 + 1 ) =3\int \frac{1}{t^2+1}d(t^2+1) = 3 ∫ t 2 + 1 1 d ( t 2 + 1 ) = 3 ln ∣ t 2 + 1 ∣ + C =3\ln |t^2+1|+C = 3 ln ∣ t 2 + 1 ∣ + C = 3 ln x 2 3 + 1 + C =3\ln x^{\frac{2}{3} +1}+C = 3 ln x 3 2 + 1 + C ∫ x 3 x + 1 3 d x \int x\sqrt[3]{3x+1}dx ∫ x 3 3 x + 1 d x 3 x + 1 3 = t , x = 1 3 t 3 − 1 3 , d x = d ( 1 3 t 3 − 1 3 ) = t 2 d t \sqrt[3]{3x+1}=t,x=\frac{1}{3}t^3-\frac{1}{3},dx=d(\frac{1}{3t^3-\frac{1}{3} })=t^2dt 3 3 x + 1 = t , x = 3 1 t 3 − 3 1 , d x = d ( 3 t 3 − 3 1 1 ) = t 2 d t = ∫ ( 1 3 t 3 − 1 3 ) t ⋅ t 2 d t =\int (\frac{1}{3}t^3-\frac{1}{3} )t\cdot t^2dt = ∫ ( 3 1 t 3 − 3 1 ) t ⋅ t 2 d t = ∫ ( 1 3 t 6 − 1 3 t 3 ) d t =\int (\frac{1}{3}t^6-\frac{1}{3}t^3)dt = ∫ ( 3 1 t 6 − 3 1 t 3 ) d t = 1 21 t 7 − 1 12 t 4 + C =\frac{1}{21}t^7-\frac{1}{12}t^4+C = 2 1 1 t 7 − 1 2 1 t 4 + C = 1 21 ( 3 x + 1 ) 7 3 − 1 12 ( 3 x + 1 ) 4 3 + C =\frac{1}{21}(3x+1)^{\frac{7}{3} }-\frac{1}{12}(3x+1)^{\frac{4}{3} }+C = 2 1 1 ( 3 x + 1 ) 3 7 − 1 2 1 ( 3 x + 1 ) 3 4 + C x m \sqrt[m]{x} m x x n \sqrt[n]{x} n x t = x m , n , [ m , n ] t=\sqrt[m,n]{x},[m,n] t = m , n x , [ m , n ] m m m n n n 最小公倍数 。∫ 1 x + x 4 d x \int \frac{1}{\sqrt{x}+\sqrt[4]{x} }dx ∫ x + 4 x 1 d x x 4 = t , x = t 4 , d x = d t 4 = 4 t 3 d t \sqrt[4]{x}=t,x=t^4,dx=dt^4=4t^3dt 4 x = t , x = t 4 , d x = d t 4 = 4 t 3 d t = ∫ 1 t 2 + t 4 t 3 d t =\int \frac{1}{t^2+t}4t^3dt = ∫ t 2 + t 1 4 t 3 d t = 4 t 2 t + 1 d t =4\frac{t^2}{t+1}dt = 4 t + 1 t 2 d t t + 1 = u , t = u − 1 , d t = d ( u − 1 ) = d u t+1=u,t=u-1,dt=d(u-1)=du t + 1 = u , t = u − 1 , d t = d ( u − 1 ) = d u 4 ∫ ( u − 1 ) 2 u d u 4\int \frac{(u-1)^2}{u}du 4 ∫ u ( u − 1 ) 2 d u = 4 ∫ u 2 − 2 u + 1 u d u =4\int \frac{u^2-2u+1}{u}du = 4 ∫ u u 2 − 2 u + 1 d u = 4 ∫ ( u − 2 + 1 u ) d x =4\int (u-2+\frac{1}{u})dx = 4 ∫ ( u − 2 + u 1 ) d x = 2 ( u ) − 8 u + 4 ln ∣ u ∣ + C =2(u)-8u+4\ln |u|+C = 2 ( u ) − 8 u + 4 ln ∣ u ∣ + C = 2 ( x 4 + 1 ) 2 − 8 ( x 3 + 1 ) + 4 ln ( x 4 + 1 ) + C =2(\sqrt[4]{x}+1)^2-8(\sqrt[3]{x}+1)+4\ln (\sqrt[4]{x}+1)+C = 2 ( 4 x + 1 ) 2 − 8 ( 3 x + 1 ) + 4 ln ( 4 x + 1 ) + C ∫ x 3 3 x + x 3 d x \int x\frac{\sqrt[3]{3} }{\sqrt{x}+\sqrt[3]{x} }dx ∫ x x + 3 x 3 3 d x x 6 = t , x = t 6 , d x = d t 6 = 6 t 5 d t \sqrt[6]{x}=t,x=t^6,dx=dt^6=6t^5dt 6 x = t , x = t 6 , d x = d t 6 = 6 t 5 d t = ∫ t 2 t 6 ⋅ ( t 3 − t 2 ) ⋅ 6 t 5 d t =\int \frac{t^2}{t^6 \cdot (t^3-t^2) }\cdot 6t^5 dt = ∫ t 6 ⋅ ( t 3 − t 2 ) t 2 ⋅ 6 t 5 d t 6 ∫ 1 t 2 + t d t 6\int\frac{1}{t^2+t}dt 6 ∫ t 2 + t 1 d t = 6 ∫ 1 t − 1 ( t + 1 ) d t =6\int \frac{1}{t}-\frac{1}{(t+1)}dt = 6 ∫ t 1 − ( t + 1 ) 1 d t = 6 ln t − 6 ln ∣ t + 1 ∣ + C =6\ln t-6\ln |t+1|+C = 6 ln t − 6 ln ∣ t + 1 ∣ + C = 6 ln ∣ t t + 1 ∣ + C =6\ln |\frac{t}{t+1}|+C = 6 ln ∣ t + 1 t ∣ + C = 6 ln ( x 6 ) 6 x 6 + 1 + C =6\ln \frac{(\sqrt[6]{x}) }{6\sqrt[6]{x}+1}+C = 6 ln 6 6 x + 1 ( 6 x ) + C a 2 − x 2 \sqrt{a^2-x^2} a 2 − x 2 x = a sin u x=a\sin u x = a sin u x 2 + a 2 \sqrt{x^2+a^2} x 2 + a 2 x = a tan u x=a\tan u x = a tan u x 2 − a 2 \sqrt{x^2-a^2} x 2 − a 2 x = a sec u x=a\sec u x = a sec u ∫ x + arcsin x 1 − x 2 d x \int \frac{x+\arcsin x}{\sqrt{1-x^2} }dx ∫ 1 − x 2 x + a r c s i n x d x = ∫ x 1 − x 2 d x + ∫ arcsin x 1 − x 2 d x =\int \frac{x}{\sqrt{1-x^2} }dx+\int \frac{\arcsin x}{\sqrt{1-x^2} }dx = ∫ 1 − x 2 x d x + ∫ 1 − x 2 a r c s i n x d x = ∫ x ⋅ 1 1 − x 2 d x + ∫ arcsin x ⋅ 1 1 − x 2 d x =\int x \cdot \frac{1}{\sqrt{1-x^2} }dx+\int \arcsin x \cdot \frac{1}{\sqrt{1-x^2} }dx = ∫ x ⋅ 1 − x 2 1 d x + ∫ arcsin x ⋅ 1 − x 2 1 d x = 1 2 ∫ 1 1 − x 2 d x 2 + ∫ arcsin x d ( arcsin x ) =\frac{1}{2} \int \frac{1}{\sqrt{1-x^2} }dx^2+\int \arcsin x d (\arcsin x ) = 2 1 ∫ 1 − x 2 1 d x 2 + ∫ arcsin x d ( arcsin x ) = 1 2 ∫ 1 1 − x 2 d ( 1 − x 2 ) + 1 2 arcsin x =\frac{1}{2} \int \frac{1}{\sqrt{1-x^2} }d(1-x^2)+\frac{1}{2}\arcsin x = 2 1 ∫ 1 − x 2 1 d ( 1 − x 2 ) + 2 1 arcsin x = 1 2 − 1 2 ⋅ 1 − x 2 + 1 2 arcsin 2 x + C =\frac{1}{2} -\frac{1}{2}\cdot \sqrt{1-x^2}+\frac{1}{2} \arcsin^2x+C = 2 1 − 2 1 ⋅ 1 − x 2 + 2 1 arcsin 2 x + C = 1 2 − 1 − x 2 + 1 2 arcsin 2 x + C =\frac{1}{2} -\sqrt{1-x^2}+\frac{1}{2}\arcsin^2x+C = 2 1 − 1 − x 2 + 2 1 arcsin 2 x + C ∫ f ( x , a x + b n ) d x \int f(x,\sqrt[n]{ax+b})dx ∫ f ( x , n a x + b ) d x t = a x + b n t=\sqrt[n]{ax+b} t = n a x + b ∫ f ( x , a x + b c x + d n ) d x \int f(x,\sqrt[n]{\frac{ax+b}{cx+d} })dx ∫ f ( x , n c x + d a x + b ) d x t = a x + b c x + d n t=\sqrt[n]{\frac{ax+b}{cx+d} } t = n c x + d a x + b ∫ f ( x , a 2 − x 2 ) d x \int f(x,\sqrt{a^2-x^2})dx ∫ f ( x , a 2 − x 2 ) d x x = a sin / x = a cos t x=a\sin / x=a\cos t x = a sin / x = a cos t ∫ f ( x , a 2 + x 2 ) d x \int f(x,\sqrt{a^2+x^2})dx ∫ f ( x , a 2 + x 2 ) d x x = a tan t x=a\tan t x = a tan t ∫ f ( x , x 2 − a 2 ) d x \int f(x,\sqrt{x^2-a^2})dx ∫ f ( x , x 2 − a 2 ) d x x = a sec t x=a\sec t x = a sec t ∫ f ( a x ) d x \int f(a^x)dx ∫ f ( a x ) d x t = a x t=a^x t = a x ∫ tan x d x = − ln ∣ cos x ∣ + C \int \tan xdx=-\ln|\cos x|+C ∫ tan x d x = − ln ∣ cos x ∣ + C ∫ cot x d x = ln ∣ sin x ∣ + C \int \cot xdx=\ln |\sin x |+C ∫ cot x d x = ln ∣ sin x ∣ + C ∫ sec x d x = ln ∣ sec x + tan x ∣ + C \int \sec xdx=\ln |\sec x+\tan x |+C ∫ sec x d x = ln ∣ sec x + tan x ∣ + C ∫ csc x d x = ln ∣ csc x − cot x ∣ + C \int \csc xdx=\ln |\csc x-\cot x |+C ∫ csc x d x = ln ∣ csc x − cot x ∣ + C ∫ 1 a 2 + x 2 d x = 1 a arctan x a + C \int \frac{1}{a^2+x^2 }dx=\frac{1}{a} \arctan \frac{x}{a}+C ∫ a 2 + x 2 1 d x = a 1 arctan a x + C
分部积分法 公式:∫ u v ′ d x = ∫ u d v = u v − ∫ u ′ v d x = u v − ∫ v d u \int uv' dx=\int udv=uv-\int u'v dx=uv-\int vdu ∫ u v ′ d x = ∫ u d v = u v − ∫ u ′ v d x = u v − ∫ v d u 反对幂指三 ∫ x arctan x d x \int x\arctan xdx ∫ x arctan x d x = ∫ arctan x ⋅ x d ( 1 2 x 2 ) =\int \arctan x \cdot xd(\frac{1}{2}x^2) = ∫ arctan x ⋅ x d ( 2 1 x 2 ) 1 2 ∫ arctan x d x 2 \frac{1}{2}\int \arctan xdx^2 2 1 ∫ arctan x d x 2 = 1 2 ( x 2 arctan x − ∫ x 2 d ( arctan x ) ) =\frac{1}{2}(x^2\arctan x-\int x^2d(\arctan x)) = 2 1 ( x 2 arctan x − ∫ x 2 d ( arctan x ) ) = 1 2 ( x 2 arctan x − ∫ x 2 ⋅ 1 1 + x 2 d x ) =\frac{1}{2}(x^2\arctan x-\int x^2\cdot \frac{1}{1+x^2}dx) = 2 1 ( x 2 arctan x − ∫ x 2 ⋅ 1 + x 2 1 d x ) = 1 2 ( x 2 arctan x − ∫ x 2 + 1 − 1 1 + x 2 d x ) =\frac{1}{2}(x^2\arctan x-\int \frac{x^2+1-1}{1+x^2}dx) = 2 1 ( x 2 arctan x − ∫ 1 + x 2 x 2 + 1 − 1 d x ) = 1 2 ( x 2 arctan x − ∫ 1 − 1 1 + x 2 d x ) =\frac{1}{2}(x^2\arctan x-\int 1-\frac{1}{1+x^2}dx) = 2 1 ( x 2 arctan x − ∫ 1 − 1 + x 2 1 d x ) = 1 2 ( x 2 arctan x − x + arctan x ) + C =\frac{1}{2}(x^2\arctan x-x+\arctan x)+C = 2 1 ( x 2 arctan x − x + arctan x ) + C ∫ arctan x d x \int \arctan xdx ∫ arctan x d x = x arctan x − ∫ x d ( arctan x ) =x\arctan x-\int xd(\arctan x) = x arctan x − ∫ x d ( arctan x ) = x arctan x − ∫ x ⋅ 1 1 + x 2 d x =x\arctan x-\int x\cdot \frac{1}{1+x^2}dx = x arctan x − ∫ x ⋅ 1 + x 2 1 d x = x arctan x − 1 2 ∫ 1 1 + x 2 d x 2 =x\arctan x-\frac{1}{2}\int \frac{1}{1+x^2}dx^2 = x arctan x − 2 1 ∫ 1 + x 2 1 d x 2 = x arctan x − 1 2 ln ( 1 + x 2 ) =x\arctan x-\frac{1}{2}\ln (1+x^2) = x arctan x − 2 1 ln ( 1 + x 2 ) ∫ x 3 ln x d x \int x^3\ln xdx ∫ x 3 ln x d x = ∫ ln x ⋅ x d ( 1 4 x 4 ) =\int \ln x \cdot xd(\frac{1}{4}x^4) = ∫ ln x ⋅ x d ( 4 1 x 4 ) = 1 4 ∫ ln x d x 4 =\frac{1}{4}\int \ln xdx^4 = 4 1 ∫ ln x d x 4 = 1 4 ( x 4 ln x − ∫ x 4 d ( ln x ) ) =\frac{1}{4}(x^4\ln x-\int x^4d(\ln x)) = 4 1 ( x 4 ln x − ∫ x 4 d ( ln x ) ) = 1 4 ( x 4 ln x − ∫ x 4 ⋅ 1 x d x ) =\frac{1}{4}(x^4\ln x-\int x^4\cdot \frac{1}{x}dx) = 4 1 ( x 4 ln x − ∫ x 4 ⋅ x 1 d x ) = 1 4 ( x 4 ln x − ∫ x 3 d x ) =\frac{1}{4}(x^4\ln x-\int x^3dx) = 4 1 ( x 4 ln x − ∫ x 3 d x ) = 1 4 x 4 ln x − 1 16 x 4 + C =\frac{1}{4}x^4\ln x-\frac{1}{16}x^4+C = 4 1 x 4 ln x − 1 6 1 x 4 + C ∫ e x sin x d x \int e^x\sin xdx ∫ e x sin x d x = ∫ e x d ( − cos x ) =\int e^xd(-\cos x) = ∫ e x d ( − cos x ) = − ∫ e x d ( cos x ) =-\int e^xd(\cos x) = − ∫ e x d ( cos x ) = − ( e x ⋅ cos x − ∫ cos x d ( e x ) ) =-(e^x \cdot \cos x-\int \cos xd(e^x)) = − ( e x ⋅ cos x − ∫ cos x d ( e x ) ) = − ( cos x ⋅ e x − ∫ cos x ⋅ e x d x ) =-(\cos x \cdot e^x-\int \cos x\cdot e^x dx) = − ( cos x ⋅ e x − ∫ cos x ⋅ e x d x ) = − cos x ⋅ e x + ∫ e x d sin x =-\cos x \cdot e^x+\int e^x d\sin x = − cos x ⋅ e x + ∫ e x d sin x = − cos x ⋅ e x + sin x ⋅ e x − ∫ sin x d e x =-\cos x \cdot e^x+\sin x \cdot e^x-\int \sin xde^x = − cos x ⋅ e x + sin x ⋅ e x − ∫ sin x d e x = − cos x ⋅ e x + sin x ⋅ e x − ∫ e x ⋅ sin x d x =-\cos x \cdot e^x+\sin x \cdot e^x-\int e^x\cdot \sin xdx = − cos x ⋅ e x + sin x ⋅ e x − ∫ e x ⋅ sin x d x ∫ e x sin x d x = − cos x ⋅ e x + sin x ⋅ e x − ∫ e x ⋅ sin x d x \int e^x\sin xdx=-\cos x \cdot e^x+\sin x \cdot e^x-\int e^x\cdot \sin xdx ∫ e x sin x d x = − cos x ⋅ e x + sin x ⋅ e x − ∫ e x ⋅ sin x d x 2 ∫ e x sin x d x = − cos x ⋅ e x − sin x ⋅ e x 2\int e^x\sin xdx=-\cos x \cdot e^x-\sin x \cdot e^x 2 ∫ e x sin x d x = − cos x ⋅ e x − sin x ⋅ e x ∫ e x sin x d x = − cos x ⋅ e x + e x ⋅ sin x 2 + C \int e^x\sin xdx =\frac{-\cos x \cdot e^x+e^x \cdot \sin x }{2}+C ∫ e x sin x d x = 2 − c o s x ⋅ e x + e x ⋅ s i n x + C
定积分 定积分的概念
概念∫ a b f ( x ) d x \int_a^b f(x)dx ∫ a b f ( x ) d x a , b a,b a , b f ( x ) f(x) f ( x )
定积分的几何意义∫ a b f ( x ) d x \int_a^b f(x)dx ∫ a b f ( x ) d x y = f ( x ) y=f(x) y = f ( x ) x x x x = a , x = b x=a,x=b x = a , x = b f ( x ) > 0 , ∫ a b f ( x ) d x > 0 f(x)>0,\int_a^b f(x)dx>0 f ( x ) > 0 , ∫ a b f ( x ) d x > 0 f ( x ) < 0 , ∫ a b f ( x ) d x < 0 f(x)<0,\int_a^b f(x)dx < 0 f ( x ) < 0 , ∫ a b f ( x ) d x < 0
定积分比较大小 f ( x ) ≥ g ( x ) f(x)\geq g(x) f ( x ) ≥ g ( x ) ∫ a b f ( x ) d x ≥ ∫ a b g ( x ) d x \int_a^b f(x)dx\geq \int_a^b g(x)dx ∫ a b f ( x ) d x ≥ ∫ a b g ( x ) d x ∫ 0 π 2 x d x \int_0^{\frac{\pi}{2} } xdx ∫ 0 2 π x d x ∫ 0 π 2 sin x d x \int_0^{\frac{\pi}{2} } \sin xdx ∫ 0 2 π sin x d x f ( x ) = x , g ( x ) = sin x f(x)=x,g(x)=\sin x f ( x ) = x , g ( x ) = sin x f ( x ) ≥ g ( x ) f(x)\geq g(x) f ( x ) ≥ g ( x ) ∫ 0 π 2 x d x > ∫ 0 π 2 sin x d x \int_0^{\frac{\pi}{2} } xdx > \int_0^{\frac{\pi}{2} } \sin xdx ∫ 0 2 π x d x > ∫ 0 2 π sin x d x
例题2:比较∫ 0 1 e x d x \int_0^1 e^xdx ∫ 0 1 e x d x ∫ 0 1 e x 2 d x \int_0^1 e^{x^2} dx ∫ 0 1 e x 2 d x x ∈ ( 0 , 1 ) x \in (0,1) x ∈ ( 0 , 1 ) x , x 2 x,x^2 x , x 2 ∫ 0 1 e x d x > ∫ 0 1 e x 2 d x \int_0^1 e^xdx > \int_0^1 e^{x^2} dx ∫ 0 1 e x d x > ∫ 0 1 e x 2 d x
定积分的性质∫ a b f ( x ) ± g ( x ) d x = ∫ a b f ( x ) d x + ∫ a b g ( x ) d x \int_a^b f(x)\pm g(x)dx=\int_a^b f(x)dx+\int_a^b g(x)dx ∫ a b f ( x ) ± g ( x ) d x = ∫ a b f ( x ) d x + ∫ a b g ( x ) d x ∫ a b k ⋅ f ( x ) d x = k ∫ a b f ( x ) d x ( k 与 x 无关 ) \int_a^b k\cdot f(x)dx=k\int_a^b f(x)dx(k与x无关) ∫ a b k ⋅ f ( x ) d x = k ∫ a b f ( x ) d x ( k 与 x 无 关 ) ∫ a b f ( x ) d x = ∫ a c f ( x ) d x + ∫ c b f ( x ) d x \int_a^b f(x)dx=\int_a^c f(x)dx+\int_c^b f(x)dx ∫ a b f ( x ) d x = ∫ a c f ( x ) d x + ∫ c b f ( x ) d x ∫ a b f ( x ) d x = − ∫ b a \int_a^b f(x)dx=-\int_b^a ∫ a b f ( x ) d x = − ∫ b a ∫ a b 1 d x + ∫ a b d x = b − a \int_a^b 1dx+\int_a^b dx=b-a ∫ a b 1 d x + ∫ a b d x = b − a f ( x ) f(x) f ( x ) [ a , b ] [a,b] [ a , b ] ∫ 0 x f ( t ) d t \int_0^x f(t)dt ∫ 0 x f ( t ) d t f ( x ) f(x) f ( x ) ∫ x b f ( t ) d t \int_x^b f(t)dt ∫ x b f ( t ) d t − f ( x ) -f(x) − f ( x ) ∫ a b f ( t ) d t \int_a^b f(t)dt ∫ a b f ( t ) d t f ( x ) f(x) f ( x ) f ( x ) f(x) f ( x ) [ a , b ] [a,b] [ a , b ] f ( x ) f(x) f ( x ) [ a , b ] [a,b] [ a , b ] ∫ 0 x f ( t ) d t \int_0^x f(t)dt ∫ 0 x f ( t ) d t ( ∫ 0 x f ( t ) d t ) ′ = f ( x ) (\int_0^x f(t)dt)'=f(x) ( ∫ 0 x f ( t ) d t ) ′ = f ( x ) ∫ x b f ( t ) d t \int_x^b f(t)dt ∫ x b f ( t ) d t ( ∫ x b f ( t ) d t ) ′ = 0 − f ( x ) (\int_x^b f(t)dt)'=0-f(x) ( ∫ x b f ( t ) d t ) ′ = 0 − f ( x ) ∫ a b f ( t ) d t \int_a^b f(t)dt ∫ a b f ( t ) d t f ( x ) f(x) f ( x ) 定积分是一个数字,所以 f ( x ) = 0 定积分是一个数字,所以f(x)=0 定 积 分 是 一 个 数 字 , 所 以 f ( x ) = 0 f ( x ) f(x) f ( x ) [ a , b ] [a,b] [ a , b ]
定积分的计算 定积分两个公式 牛顿-莱布尼茨公式:∫ a b f ( x ) d x = F ( x ) ∣ b a = F ( b ) − F ( a ) \int_a^b f(x)dx=F(x)|\begin{matrix}b\\a\end{matrix}=F(b)-F(a) ∫ a b f ( x ) d x = F ( x ) ∣ b a = F ( b ) − F ( a ) ∫ a b u v ′ d x = ∫ a b u d v = u v ∣ b a − ∫ a b v u ′ d x \int_a^b uv' dx=\int_a^b udv=uv|\begin{matrix}b\\a\end{matrix}-\int_a^b vu' dx ∫ a b u v ′ d x = ∫ a b u d v = u v ∣ b a − ∫ a b v u ′ d x ∫ 0 1 ( x 2 + x + 2 ) d x \int_0^1 (x^2+x+2)dx ∫ 0 1 ( x 2 + x + 2 ) d x = ( 1 3 x 3 + 1 2 x 2 + 2 x ) ∣ 1 0 =(\frac{1}{3}x^3+\frac{1}{2}x^2+2x)|\begin{matrix}1\\0\end{matrix} = ( 3 1 x 3 + 2 1 x 2 + 2 x ) ∣ 1 0 = 1 3 + 1 2 + 2 − 0 = 17 6 =\frac{1}{3}+\frac{1}{2}+2-0=\frac{17}{6} = 3 1 + 2 1 + 2 − 0 = 6 1 7 ∫ 0 π 2 cos 2 x cos x − sin x d x \int_0^{\frac{\pi}{2}} \frac{\cos 2x}{\cos x-\sin x}dx ∫ 0 2 π c o s x − s i n x c o s 2 x d x = ∫ 0 π 2 ( cos x − sin x ) ⋅ ( sin x + cos x ) cos x − sin x d x =\int_0^{\frac{\pi}{2}} \frac{(\cos x-\sin x)\cdot (\sin x+\cos x )}{\cos x-\sin x}dx = ∫ 0 2 π c o s x − s i n x ( c o s x − s i n x ) ⋅ ( s i n x + c o s x ) d x = ∫ 0 π 2 sin x + cos x d x =\int_0^{\frac{\pi}{2}} \sin x+\cos x dx = ∫ 0 2 π sin x + cos x d x = ( − cos x + sin x ) ∣ π 2 0 =(-\cos x+\sin x)|\begin{matrix}\frac{\pi}{2}\\0\end{matrix} = ( − cos x + sin x ) ∣ 2 π 0 = ( 0 + 1 ) − ( − 1 + 0 ) =(0+1)-(-1+0) = ( 0 + 1 ) − ( − 1 + 0 ) = 2 =2 = 2 ∫ 1 2 e 1 x ⋅ 1 x 2 d x \int_1^2 e^{\frac{1}{x} }\cdot \frac{1}{x^2}dx ∫ 1 2 e x 1 ⋅ x 2 1 d x = ∫ 1 2 e 1 x ⋅ ( − 1 x ) ′ d x =\int_1^2 e^{\frac{1}{x} }\cdot (-\frac{1}{x})'dx = ∫ 1 2 e x 1 ⋅ ( − x 1 ) ′ d x = − ∫ 1 2 e 1 x d ( 1 x ) =-\int_1^2 e^{\frac{1}{x} }d(\frac{1}{x}) = − ∫ 1 2 e x 1 d ( x 1 ) = − e 1 x ∣ 2 1 =-e^{\frac{1}{x} }|\begin{matrix}2\\1\end{matrix} = − e x 1 ∣ 2 1 = − e 1 2 + e =-e^{\frac{1}{2} }+e = − e 2 1 + e ∫ 0 1 x ⋅ e − x d x \int_0^1 x\cdot e^{-x}dx ∫ 0 1 x ⋅ e − x d x = ∫ 0 1 x d ( − e − x ) =\int_0^1 x d(-e^{-x}) = ∫ 0 1 x d ( − e − x ) = − ( x ⋅ e − x ∣ 1 0 − ∫ 0 1 e − x d x ) =-(x\cdot e^{-x}|\begin{matrix}1\\0\end{matrix}-\int_0^1e^{-x}dx) = − ( x ⋅ e − x ∣ 1 0 − ∫ 0 1 e − x d x ) = − ( x e − x ∣ 1 0 + e − x ∣ 1 0 ) =-(xe^{-x}|\begin{matrix}1\\0\end{matrix}+e^{-x}|\begin{matrix}1\\0\end{matrix}) = − ( x e − x ∣ 1 0 + e − x ∣ 1 0 ) = − ( e − 1 + e − 1 − 1 =-(e^{-1}+e^{-1}-1 = − ( e − 1 + e − 1 − 1 = − 2 e − 1 + 1 = 1 − 2 e =-2e^{-1}+1=1-\frac{2}{e} = − 2 e − 1 + 1 = 1 − e 2
定积分四个运算技巧
定积分偶倍奇零(条件:区间对称 ) ∫ − a a f ( x ) d x = { 2 ∫ 0 a f ( x ) d x , f ( x ) 为偶函数 0 , f ( x ) 为奇函数 \int_{-a}^{a} f(x)dx=\left\{\begin{matrix}2\int_{0}^{a} f(x)dx,f(x)为偶函数\\0,f(x)为奇函数\end{matrix}\right. ∫ − a a f ( x ) d x = { 2 ∫ 0 a f ( x ) d x , f ( x ) 为 偶 函 数 0 , f ( x ) 为 奇 函 数 { 常见偶函数: C , x 偶数 , ∣ x ∣ , cos x , f ( x ) + f ( − x ) 常见奇函数: x 奇数 , sin x , arctan x , f ( x ) − f ( − x ) \left\{\begin{matrix}常见偶函数:C,x^{偶数},|x|,\cos x,f(x)+f(-x) \\常见奇函数:x^{奇数},\sin x,\arctan x,f(x)-f(-x)\end{matrix}\right. { 常 见 偶 函 数 : C , x 偶 数 , ∣ x ∣ , cos x , f ( x ) + f ( − x ) 常 见 奇 函 数 : x 奇 数 , sin x , arctan x , f ( x ) − f ( − x ) ∫ − 1 1 ( x 3 cos x + 1 ) d x = ( D ) \int_{-1}^{1} (x^3\cos x+1)dx=(D) ∫ − 1 1 ( x 3 cos x + 1 ) d x = ( D ) A . 0 B . 1 2 C . 1 D . 2 A. 0 B. \frac{1}{2} C. 1 D. 2 A . 0 B . 2 1 C . 1 D . 2 x 3 cos x x^3\cos x x 3 cos x 2 ∫ 0 1 1 d x = 2 2\int_0^1 1dx=2 2 ∫ 0 1 1 d x = 2 f ( x ) f(x) f ( x ) [ − l , l ] [-l,l] [ − l , l ] ∫ − l l f ( x ) − f ( − x ) d x = ( 0 ) \int_{-l}^{l} f(x)-f(-x)dx=(0) ∫ − l l f ( x ) − f ( − x ) d x = ( 0 ) f ( x ) − f ( − x ) f(x)-f(-x) f ( x ) − f ( − x ) 0 0 0 ∫ − 1 1 2 + sin x 1 + x 2 d x \int_{-1}^{1} \frac{2+\sin x}{1+x^2}dx ∫ − 1 1 1 + x 2 2 + s i n x d x = ∫ − 1 1 2 1 + x 2 d x + ∫ − 1 1 sin x 1 + x 2 =\int_{-1}^{1} \frac{2}{1+x^2}dx+\int_{-1}^{1}\frac{\sin x}{1+x^2} = ∫ − 1 1 1 + x 2 2 d x + ∫ − 1 1 1 + x 2 s i n x 2 1 + x 2 \frac{2}{1+x^2} 1 + x 2 2 sin x 1 + x 2 \frac{\sin x}{1+x^2} 1 + x 2 s i n x 2 ⋅ 2 ∫ 0 1 1 1 + x 2 d x + 0 = 4 arctan x ∣ 1 0 = 4 ( arctan 1 − arctan 0 ) = π 2\cdot 2\int_0^1 \frac{1}{1+x^2}dx+0=4\arctan x|\begin{matrix}1\\0\end{matrix}=4(\arctan 1-\arctan 0)=\pi 2 ⋅ 2 ∫ 0 1 1 + x 2 1 d x + 0 = 4 arctan x ∣ 1 0 = 4 ( arctan 1 − arctan 0 ) = π ∫ − π π ( 1 + cos x + ∣ x ∣ ⋅ x ) d x \int_{-\pi}^{\pi} (\sqrt{1+\cos x}+|x|\cdot x)dx ∫ − π π ( 1 + cos x + ∣ x ∣ ⋅ x ) d x 1 + cos x \sqrt{1+\cos x} 1 + cos x ∣ x ∣ ⋅ x |x|\cdot x ∣ x ∣ ⋅ x = 2 ∫ 0 π 1 + cos x d x =2\int_{0}^{\pi} \sqrt{1+\cos x}dx = 2 ∫ 0 π 1 + cos x d x = 2 ∫ 0 π 2 ⋅ cos x 2 d x =2\int_{0}^{\pi} \sqrt{2}\cdot \cos \frac{x}{2}dx = 2 ∫ 0 π 2 ⋅ cos 2 x d x = 2 ⋅ 2 2 ∫ 0 π cos x 2 d ( x 2 ) =2\cdot 2\sqrt{2} \int_{0}^{\pi} \cos \frac{x}{2}d(\frac{x}{2}) = 2 ⋅ 2 2 ∫ 0 π cos 2 x d ( 2 x ) = 4 2 ∫ 0 π cos x 2 d ( x 2 ) =4\sqrt{2}\int_{0}^{\pi} \cos \frac{x}{2} d(\frac{x}{2}) = 4 2 ∫ 0 π cos 2 x d ( 2 x ) = 4 2 sin x 2 ∣ π 0 =4\sqrt{2} \sin \frac{x}{2}|\begin{matrix}\pi\\0\end{matrix} = 4 2 sin 2 x ∣ π 0 = 4 2 ⋅ ( sin π 2 − sin 0 ) =4\sqrt{2}\cdot(\sin \frac{\pi}{2}-\sin 0) = 4 2 ⋅ ( sin 2 π − sin 0 ) = 4 2 =4\sqrt{2} = 4 2
定积分点火公式(华里氏公式)( 0 , π 2 ) (0,\frac{\pi}{2}) ( 0 , 2 π ) ∫ 0 π 2 sin n x d x = ∫ 0 π 2 cos n x d x = { n − 1 n ⋅ n − 3 n − 2 … 1 2 ⋅ π 2 , n 为偶数 n − 1 n ⋅ n − 3 n − 2 … 2 3 ⋅ 1 , n 为奇数 \int_{0}^{\frac{\pi }{2} }\sin ^nxdx=\int_{0}^{\frac{\pi }{2} }\cos ^nxdx=\left\{\begin{matrix}\frac{n-1}{n}\cdot \frac{n-3}{n-2}\dots \frac{1}{2}\cdot \frac{\pi }{2} ,n为偶数 \\\frac{n-1}{n}\cdot \frac{n-3}{n-2}\dots \frac{2}{3}\cdot 1 ,n为奇数 \end{matrix}\right. ∫ 0 2 π sin n x d x = ∫ 0 2 π cos n x d x = { n n − 1 ⋅ n − 2 n − 3 … 2 1 ⋅ 2 π , n 为 偶 数 n n − 1 ⋅ n − 2 n − 3 … 3 2 ⋅ 1 , n 为 奇 数 ∫ 0 π sin n x d x = 2 ∫ 0 π 2 sin n x d x {\color{Red} \int_{0}^{\pi }\sin ^n xdx=2\int_{0}^{\frac{\pi }{2} } \sin ^n xdx } ∫ 0 π s i n n x d x = 2 ∫ 0 2 π s i n n x d x ∫ 0 π 2 cos 6 x d x \int_{0}^{\frac{\pi }{2} }\cos ^6xdx ∫ 0 2 π cos 6 x d x = 5 6 ⋅ 3 4 ⋅ 1 2 ⋅ π 2 = 5 π 64 =\frac{5}{6}\cdot \frac{3}{4}\cdot \frac{1}{2}\cdot \frac{\pi }{2}=\frac{5\pi }{64} = 6 5 ⋅ 4 3 ⋅ 2 1 ⋅ 2 π = 6 4 5 π ∫ 0 π 2 sin 5 x d x \int_{0}^{\frac{\pi }{2} }\sin ^5xdx ∫ 0 2 π sin 5 x d x = 4 5 ⋅ 2 3 ⋅ 1 2 ⋅ 1 = 4 15 =\frac{4}{5}\cdot \frac{2}{3}\cdot \frac{1}{2}\cdot 1=\frac{4}{15} = 5 4 ⋅ 3 2 ⋅ 2 1 ⋅ 1 = 1 5 4 ∫ − π 2 π 2 ( sin 4 θ + cos 3 θ ) d θ \int_{-\frac{\pi}{2} }^{\frac{\pi }{2} }(\sin ^4\theta +\cos ^3\theta )d\theta ∫ − 2 π 2 π ( sin 4 θ + cos 3 θ ) d θ = 2 ∫ 0 π 2 ( sin 4 θ + cos 3 θ ) d θ =2\int_0^{\frac{\pi}{2} }(\sin ^4\theta +\cos ^3\theta )d\theta = 2 ∫ 0 2 π ( sin 4 θ + cos 3 θ ) d θ = 2 ( 3 4 ⋅ 1 2 ⋅ π 2 + 2 3 ⋅ 1 ) =2(\frac{3}{4}\cdot \frac{1}{2}\cdot \frac{\pi}{2} +\frac{2}{3}\cdot 1) = 2 ( 4 3 ⋅ 2 1 ⋅ 2 π + 3 2 ⋅ 1 ) = 3 π 8 + 4 3 =\frac{3\pi}{8}+\frac{4}{3} = 8 3 π + 3 4
定积分求1/4圆面积∫ 0 a a 2 − x 2 d x = 1 4 π a 2 \int_{0}^{a} \sqrt{a^2-x^2}dx=\frac{1}{4}\pi a^2 ∫ 0 a a 2 − x 2 d x = 4 1 π a 2 ∫ 0 2 4 − x 2 d x = ∫ 0 2 2 2 − x 2 d x = 1 4 π ⋅ 4 = π \int_{0}^{2} \sqrt{4-x^2}dx=\int_{0}^{2}\sqrt{2^2-x^2}dx=\frac{1}{4}\pi \cdot 4=\pi ∫ 0 2 4 − x 2 d x = ∫ 0 2 2 2 − x 2 d x = 4 1 π ⋅ 4 = π ∫ − a a ( b + x ) a 2 − x 2 d x \int_{-a}^{a} (b+x)\sqrt{a^2-x^2}dx ∫ − a a ( b + x ) a 2 − x 2 d x = ∫ − a a b a 2 − x 2 + x a 2 − x 2 d x =\int_{-a}^{a} b\sqrt{a^2-x^2}+x\sqrt{a^2-x^2}dx = ∫ − a a b a 2 − x 2 + x a 2 − x 2 d x = ∫ − a a b a 2 − x 2 d x =\int_{-a}^{a} b\sqrt{a^2-x^2}dx = ∫ − a a b a 2 − x 2 d x = 2 b ∫ 0 a a 2 − x 2 d x =2b\int_{0}^{a}\sqrt{a^2-x^2}dx = 2 b ∫ 0 a a 2 − x 2 d x = 2 b ⋅ 1 4 π a 2 = 1 2 π a 2 =2b\cdot \frac{1}{4}\pi a^2=\frac{1}{2}\pi a^2 = 2 b ⋅ 4 1 π a 2 = 2 1 π a 2 f ( x ) = 3 x − 1 − x 2 − ∫ 0 1 f ( x ) d x ,求 f ( x ) f(x)=3x-\sqrt{1-x^2}-\int_{0}^{1} f(x)dx,求f(x) f ( x ) = 3 x − 1 − x 2 − ∫ 0 1 f ( x ) d x , 求 f ( x ) ∫ 0 1 f ( x ) d x = A \int_{0}^{1} f(x)dx=A ∫ 0 1 f ( x ) d x = A f ( x ) = 3 x − 1 − x 2 − A f(x)=3x-\sqrt{1-x^2}-A f ( x ) = 3 x − 1 − x 2 − A ∫ 0 1 f ( x ) d x = ∫ 0 1 3 x d x ∫ 0 1 1 − x 2 d x − ∫ 0 1 A d x \int_{0}^{1}f(x)dx=\int_{0}^{1} 3xdx\int_{0}^{1} \sqrt{1-x^2}dx-\int_{0}^{1}Adx ∫ 0 1 f ( x ) d x = ∫ 0 1 3 x d x ∫ 0 1 1 − x 2 d x − ∫ 0 1 A d x A = 3 1 2 ∣ 1 0 − π 4 − A x ∣ 1 0 A=3\frac{1}{2}|\begin{matrix}1\\0\end{matrix} -\frac{\pi}{4} -Ax|\begin{matrix}1\\0\end{matrix} A = 3 2 1 ∣ 1 0 − 4 π − A x ∣ 1 0 A = 3 ⋅ 1 2 − 1 4 π − A A=3\cdot \frac{1}{2}-\frac{1}{4}\pi -A A = 3 ⋅ 2 1 − 4 1 π − A 2 A = 3 2 − 1 4 π 2A=\frac{3}{2}-\frac{1}{4}\pi 2 A = 2 3 − 4 1 π A = 3 4 − 1 8 π A=\frac{3}{4}-\frac{1}{8}\pi A = 4 3 − 8 1 π f ( x ) = 3 x − 1 − x 2 − 3 4 + 1 8 π f(x)=3x-\sqrt{1-x^2}-\frac{3}{4}+\frac{1}{8}\pi f ( x ) = 3 x − 1 − x 2 − 4 3 + 8 1 π
定积分换元法 换元类型 { 1 ) . 无理根式代换 2 ) . 三角代换 换元类型\left\{\begin{matrix}1).无理根式代换\\2).三角代换\end{matrix}\right. 换 元 类 型 { 1 ) . 无 理 根 式 代 换 2 ) . 三 角 代 换 定积分换元换限 ∫ 1 4 1 x ( 1 + x ) d x \int_{1}^{4} \frac{1}{x(1+\sqrt{x}) }dx ∫ 1 4 x ( 1 + x ) 1 d x x = t , x = t 2 , d x = 2 t d t \sqrt{x}=t,x=t^2,dx=2tdt x = t , x = t 2 , d x = 2 t d t x = 4 , t = 2 x=4,t=2 x = 4 , t = 2 x = 1 , t = 1 x=1,t=1 x = 1 , t = 1 = ∫ 1 2 1 t 2 ( 1 + t ) 2 t d t =\int_{1}^{2} \frac{1}{t^2(1+t)}2tdt = ∫ 1 2 t 2 ( 1 + t ) 1 2 t d t = 2 ∫ 1 2 1 t ( 1 + t ) d t =2\int_{1}^{2} \frac{1}{t(1+t)}dt = 2 ∫ 1 2 t ( 1 + t ) 1 d t = 2 ∫ 1 2 1 t − 1 1 + t d t =2\int_{1}^{2} \frac{1}{t}-\frac{1}{1+t}dt = 2 ∫ 1 2 t 1 − 1 + t 1 d t = 2 ( ln t − ln ∣ 1 + t ∣ ) ∣ 2 1 =2(\ln t-\ln |1+t|)|\begin{matrix}2\\1\end{matrix} = 2 ( ln t − ln ∣ 1 + t ∣ ) ∣ 2 1 = 2 ln 2 3 − 2 ln 1 2 =2\ln \frac{2}{3}-2\ln \frac{1}{2} = 2 ln 3 2 − 2 ln 2 1 = 2 ln 4 3 =2\ln \frac{4}{3} = 2 ln 3 4 ∫ 0 1 x 2 ⋅ 1 − x 2 d x \int_{0}^{1} x^2 \cdot \sqrt{1-x^2}dx ∫ 0 1 x 2 ⋅ 1 − x 2 d x x = sin t , d x = cos t d t x=\sin t,dx=\cos tdt x = sin t , d x = cos t d t x = 1 , t = π 2 x=1,t=\frac{\pi}{2} x = 1 , t = 2 π x = 0 , t = 0 x=0,t=0 x = 0 , t = 0 = ∫ 0 π 2 sin 2 t ⋅ 1 − s i n 2 t ⋅ cos t d t =\int_{0}^{\frac{\pi}{2} } \sin ^2t\cdot \sqrt{1-sin^2t} \cdot \cos tdt = ∫ 0 2 π sin 2 t ⋅ 1 − s i n 2 t ⋅ cos t d t = ∫ 0 π 2 sin 2 t ⋅ cos 2 t d t =\int_{0}^{\frac{\pi}{2} } \sin ^2t\cdot \cos ^2tdt = ∫ 0 2 π sin 2 t ⋅ cos 2 t d t = ∫ 0 π 2 ( 1 − cos 2 t ) ⋅ cos 2 t d t =\int_{0}^{\frac{\pi}{2} } (1-\cos ^2t)\cdot \cos ^2tdt = ∫ 0 2 π ( 1 − cos 2 t ) ⋅ cos 2 t d t = ∫ 0 π 2 cos 2 t − cos 4 t d t =\int_{0}^{\frac{\pi}{2} } \cos ^2t-\cos ^4tdt = ∫ 0 2 π cos 2 t − cos 4 t d t = 1 2 ⋅ π 2 − 3 4 ⋅ 1 2 ⋅ π 2 =\frac{1}{2}\cdot \frac{\pi}{2}-\frac{3}{4}\cdot \frac{1}{2}\cdot \frac{\pi}{2} = 2 1 ⋅ 2 π − 4 3 ⋅ 2 1 ⋅ 2 π = π 16 =\frac{\pi}{16} = 1 6 π
分段函数定积分 ∫ a b f ( x ) d x = ∫ a x 0 f ( x ) d x + ∫ b x 0 f ( x ) d x \int_{a}^{b}f(x)dx=\int_{a}^{x_0}f(x)dx+\int_{b}^{x_0}f(x)dx ∫ a b f ( x ) d x = ∫ a x 0 f ( x ) d x + ∫ b x 0 f ( x ) d x 注:遇到分段函数定积分,从分段点分开单独求左侧和右侧的积分,再相加。f ( x ) = { e x , x ≤ 1 ln x , x > 1 求 ∫ 0 e f ( x ) d x f(x)=\left\{\begin{matrix}e^x,x\le 1\\\ln x,x>1\end{matrix}\right.求\int_{0}^{e}f(x)dx f ( x ) = { e x , x ≤ 1 ln x , x > 1 求 ∫ 0 e f ( x ) d x ∫ 0 e f ( x ) d x \int_{0}^{e}f(x)dx ∫ 0 e f ( x ) d x = ∫ 0 1 e x d x + ∫ 1 e ln x d x =\int_{0}^{1}e^xdx+\int_{1}^{e}\ln xdx = ∫ 0 1 e x d x + ∫ 1 e ln x d x = e x ∣ 1 0 + ( x ⋅ ln x ) ∣ e 1 − ∫ 1 e x ⋅ 1 x d x =e^x|\begin{matrix}1\\0\end{matrix}+(x \cdot \ln x)|\begin{matrix}e\\1\end{matrix}-\int_{1}^{e}x \cdot \frac{1}{x}dx = e x ∣ 1 0 + ( x ⋅ ln x ) ∣ e 1 − ∫ 1 e x ⋅ x 1 d x = e − 1 + e − 0 − x ∣ e 1 =e-1+e-0-x|\begin{matrix}e\\1\end{matrix} = e − 1 + e − 0 − x ∣ e 1 = e =e = e f ( x ) = { 1 + x 2 , x < 1 e x , x ≥ 1 求 ∫ 1 2 2 f ( 1 − x ) d x f(x)=\left\{\begin{matrix}1+x^2,x<1\\e^x,x\ge 1\end{matrix}\right.求\int_{\frac{1}{2} }^{2}f(1-x)dx f ( x ) = { 1 + x 2 , x < 1 e x , x ≥ 1 求 ∫ 2 1 2 f ( 1 − x ) d x 换元 ,令1 − x = t , x = 1 − t , d x = − d t 1-x=t,x=1-t,dx=-dt 1 − x = t , x = 1 − t , d x = − d t x = 1 2 , t = 1 2 x=\frac{1}{2} ,t=\frac{1}{2} x = 2 1 , t = 2 1 x = 2 , t = − 1 x=2,t=-1 x = 2 , t = − 1 = − ∫ 1 2 − 1 f ( t ) d t =-\int_{\frac{1}{2} }^{-1}f(t)dt = − ∫ 2 1 − 1 f ( t ) d t = ∫ − 1 1 2 f ( t ) d t =\int_{-1}^{\frac{1}{2} }f(t)dt = ∫ − 1 2 1 f ( t ) d t = − ∫ − 1 0 f ( t ) d t + ∫ 0 1 2 f ( t ) d t =-\int_{-1}^{0}f(t)dt+\int_{0}^{\frac{1}{2} }f(t)dt = − ∫ − 1 0 f ( t ) d t + ∫ 0 2 1 f ( t ) d t = ∫ − 1 0 ( 1 + t 2 ) d t + ∫ 0 1 2 e t d t =\int_{-1}^{0}(1+t^2)dt+\int_{0}^{\frac{1}{2} }e^tdt = ∫ − 1 0 ( 1 + t 2 ) d t + ∫ 0 2 1 e t d t = ( t + 1 3 t 3 ) ∣ 0 − 1 + e t ∣ 1 2 0 =(t+\frac{1}{3}t^3)|\begin{matrix}0\\-1\end{matrix}+e^t|\begin{matrix}\frac{1}{2}\\0\end{matrix} = ( t + 3 1 t 3 ) ∣ 0 − 1 + e t ∣ 2 1 0 = 0 − ( − 1 − 1 3 ) + e 1 2 − e 0 =0-(-1-\frac{1}{3})+e^{\frac{1}{2} }-e^0 = 0 − ( − 1 − 3 1 ) + e 2 1 − e 0 = 1 3 + e 1 2 − 1 =\frac{1}{3}+e^{\frac{1}{2} }-1 = 3 1 + e 2 1 − 1
定积分等式证明 积分区间再现公式:∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x \int_{a}^{b} f(x)dx=\int_{a}^{b} f(a+b-x)dx ∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x a + b − x = t , x = a + b − t , d x = − d t a+b-x=t,x=a+b-t,dx=-dt a + b − x = t , x = a + b − t , d x = − d t x = a , t = b x=a,t=b x = a , t = b x = b , t = a x=b,t=a x = b , t = a ∫ a b f ( a + b − x ) d x = − ∫ b a f ( t ) d t = ∫ a b f ( t ) d t \int_{a}^{b} f(a+b-x)dx=-\int_{b}^{a} f(t)dt=\int_{a}^{b}f(t)dt ∫ a b f ( a + b − x ) d x = − ∫ b a f ( t ) d t = ∫ a b f ( t ) d t ∫ 0 1 x m ( 1 − x ) n d x = ∫ 0 1 x n ( 1 − x ) m d x \int_{0}^{1} x^m(1-x)^ndx=\int_{0}^{1} x^n(1-x)^mdx ∫ 0 1 x m ( 1 − x ) n d x = ∫ 0 1 x n ( 1 − x ) m d x ∵ ∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x \because \int_{a}^{b}f(x)dx=\int_{a}^{b}f(a+b-x)dx ∵ ∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x ∫ 0 1 x m ( 1 − x ) n d x = ∫ 0 1 ( 1 + 0 − x ) n [ 1 − ( 1 + 0 − x ) ] m d x \int_{0}^{1} x^m(1-x)^ndx=\int_{0}^{1} (1+0-x)^n[1-(1+0-x)]^mdx ∫ 0 1 x m ( 1 − x ) n d x = ∫ 0 1 ( 1 + 0 − x ) n [ 1 − ( 1 + 0 − x ) ] m d x ∫ 0 1 x m ( 1 − x ) n d x = ∫ 0 1 ( 1 − x ) m ⋅ x n d x \int_{0}^{1} x^m(1-x)^ndx=\int_{0}^{1} (1-x)^m\cdot x^ndx ∫ 0 1 x m ( 1 − x ) n d x = ∫ 0 1 ( 1 − x ) m ⋅ x n d x ∫ 0 π 2 f ( sin x ) d x = ∫ 0 π 2 f ( cos x ) \int_{0}^{\frac{\pi }{2} } f(\sin x)dx=\int_{0}^{\frac{\pi }{2} }f(\cos x) ∫ 0 2 π f ( sin x ) d x = ∫ 0 2 π f ( cos x ) ∵ ∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x \because \int_{a}^{b}f(x)dx=\int_{a}^{b}f(a+b-x)dx ∵ ∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x ∫ 0 π 2 f ( sin x ) d x = ∫ 0 π 2 f [ sin ( π 2 − x ) ] \int_{0}^{\frac{\pi }{2} } f(\sin x)dx=\int_{0}^{\frac{\pi }{2} }f[\sin (\frac{\pi }{2}-x)] ∫ 0 2 π f ( sin x ) d x = ∫ 0 2 π f [ sin ( 2 π − x ) ] ∫ 0 π 2 f ( sin x ) d x = ∫ 0 π 2 f ( cos x ) \int_{0}^{\frac{\pi }{2} } f(\sin x)dx=\int_{0}^{\frac{\pi }{2} }f(\cos x) ∫ 0 2 π f ( sin x ) d x = ∫ 0 2 π f ( cos x ) 奇变偶不变,符号看象限 公式。∫ 0 π f ( sin x ) d x = π 2 ∫ 0 π f ( sin x ) \int_{0}^{\pi} f(\sin x)dx=\frac{\pi }{2} \int_{0}^{\pi }f(\sin x) ∫ 0 π f ( sin x ) d x = 2 π ∫ 0 π f ( sin x ) ∵ ∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x \because \int_{a}^{b}f(x)dx=\int_{a}^{b}f(a+b-x)dx ∵ ∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x ∫ 0 π x ⋅ f ( sin x ) d x = ∫ 0 π ( π − x ) ⋅ f [ sin ( π − x ) ] d x \int_{0}^{\pi} x \cdot f(\sin x)dx=\int_{0}^{\pi} (\pi-x)\cdot f[\sin (\pi-x)]dx ∫ 0 π x ⋅ f ( sin x ) d x = ∫ 0 π ( π − x ) ⋅ f [ sin ( π − x ) ] d x = ∫ 0 π ( π − x ) ⋅ f ( sin x ) d x =\int_{0}^{\pi} (\pi-x)\cdot f(\sin x)dx = ∫ 0 π ( π − x ) ⋅ f ( sin x ) d x = ∫ 0 π π ⋅ f ( sin x ) d x − ∫ 0 π x ⋅ f ( sin x ) d x =\int_{0}^{\pi}\pi \cdot f(\sin x)dx-\int_{0}^{\pi}x \cdot f(\sin x)dx = ∫ 0 π π ⋅ f ( sin x ) d x − ∫ 0 π x ⋅ f ( sin x ) d x ⟹ 2 ∫ 0 π x ⋅ f ( sin x ) d x = π ∫ 0 π f ( sin x ) d x \Longrightarrow 2\int_{0}^{\pi} x\cdot f(\sin x)dx=\pi \int_{0}^{\pi}f(\sin x)dx ⟹ 2 ∫ 0 π x ⋅ f ( sin x ) d x = π ∫ 0 π f ( sin x ) d x ⟹ ∫ 0 π x ⋅ f ( sin x ) d x = π 2 ∫ 0 π f ( sin x ) d x \Longrightarrow \int_{0}^{\pi} x\cdot f(\sin x)dx=\frac{\pi}{2} \int_{0}^{\pi}f(\sin x)dx ⟹ ∫ 0 π x ⋅ f ( sin x ) d x = 2 π ∫ 0 π f ( sin x ) d x ∫ 0 π 2 sin 3 x sin x + cos x d x = ∫ 0 π 2 cos 3 x sin x + cos x d x \int_{0}^{\frac{\pi}{2} } \frac{\sin ^3x}{\sin x+\cos x}dx=\int_{0}^{\frac{\pi}{2} } \frac{\cos ^3x}{\sin x+\cos x}dx ∫ 0 2 π s i n x + c o s x s i n 3 x d x = ∫ 0 2 π s i n x + c o s x c o s 3 x d x ∫ 0 π 2 sin 3 x sin x + cos x d x \int_{0}^{\frac{\pi}{2} } \frac{\sin ^3x}{\sin x+\cos x}dx ∫ 0 2 π s i n x + c o s x s i n 3 x d x ∵ ∫ 0 π 2 sin 3 x sin x + cos x d x \because \int_{0}^{\frac{\pi }{2} }\frac{\sin ^3x}{\sin x+\cos x}dx ∵ ∫ 0 2 π s i n x + c o s x s i n 3 x d x = ∫ 0 π 2 sin 3 ( π 2 − x ) sin ( π 2 − x ) + cos ( π 2 − x ) d x =\int_{0}^{\frac{\pi }{2} }\frac{\sin ^3(\frac{\pi }{2}-x)}{\sin (\frac{\pi }{2}-x)+\cos (\frac{\pi }{2}-x)}dx = ∫ 0 2 π s i n ( 2 π − x ) + c o s ( 2 π − x ) s i n 3 ( 2 π − x ) d x = ∫ 0 π 2 cos 3 x sin x + cos x d x =\int_{0}^{\frac{\pi }{2} }\frac{\cos ^3x}{\sin x+\cos x}dx = ∫ 0 2 π s i n x + c o s x c o s 3 x d x ∫ 0 π 2 sin 3 x sin x + cos x d x + ∫ 0 π 2 cos 3 x sin x + cos x d x \int_{0}^{\frac{\pi }{2} }\frac{\sin ^3x}{\sin x+\cos x}dx+\int_{0}^{\frac{\pi }{2} }\frac{\cos ^3x}{\sin x+\cos x}dx ∫ 0 2 π s i n x + c o s x s i n 3 x d x + ∫ 0 2 π s i n x + c o s x c o s 3 x d x = 2 ∫ 0 π 2 sin 3 x sin x + cos x d x =2\int_{0}^{\frac{\pi }{2} }\frac{\sin ^3x}{\sin x+\cos x}dx = 2 ∫ 0 2 π s i n x + c o s x s i n 3 x d x ∫ 0 π 2 sin 3 x sin x + cos x = 1 2 ⋅ [ ∫ 0 π 2 sin 3 x + cos 3 x sin x + cos x d x ] \int_{0}^{\frac{\pi }{2} }\frac{\sin ^3x}{\sin x+\cos x}=\frac{1}{2}\cdot [\int_{0}^{\frac{\pi }{2} }\frac{\sin ^3x+\cos ^3x}{\sin x+\cos x}dx] ∫ 0 2 π s i n x + c o s x s i n 3 x = 2 1 ⋅ [ ∫ 0 2 π s i n x + c o s x s i n 3 x + c o s 3 x d x ] = 1 2 ∫ 0 π 2 ( sin x + cos x ) ⋅ ( sin 2 x − sin x cos x + cos 2 ) sin x + cos x d x =\frac{1}{2}\int_{0}^{\frac{\pi }{2} }\frac{(\sin x+\cos x)\cdot (\sin ^2x-\sin x\cos x+\cos ^2)}{\sin x+\cos x}dx = 2 1 ∫ 0 2 π s i n x + c o s x ( s i n x + c o s x ) ⋅ ( s i n 2 x − s i n x c o s x + c o s 2 ) d x = 1 2 ∫ 0 π 2 1 − sin x cos x d x =\frac{1}{2}\int_{0}^{\frac{\pi }{2} } 1-\sin x \cos xdx = 2 1 ∫ 0 2 π 1 − sin x cos x d x = 1 2 ∫ 0 π 2 1 d x − 1 2 ∫ 0 π 2 sin x cos x d x =\frac{1}{2}\int_{0}^{\frac{\pi }{2} } 1dx-\frac{1}{2}\int_{0}^{\frac{\pi }{2} }\sin x \cos xdx = 2 1 ∫ 0 2 π 1 d x − 2 1 ∫ 0 2 π sin x cos x d x = 1 2 ⋅ x ∣ π 2 0 − 1 2 ∫ 0 π 2 sin x sin x =\frac{1}{2}\cdot x|\begin{matrix}\frac{\pi }{2}\\0\end{matrix}-\frac{1}{2}\int_{0}^{\frac{\pi }{2} }\sin x\sin x = 2 1 ⋅ x ∣ 2 π 0 − 2 1 ∫ 0 2 π sin x sin x = 1 2 ⋅ π 2 − 1 2 ⋅ 1 2 ( sin x ) 2 ∣ π 2 0 =\frac{1}{2}\cdot \frac{\pi }{2}-\frac{1}{2} \cdot \frac{1}{2}(\sin x)^2|\begin{matrix}\frac{\pi }{2}\\0\end{matrix} = 2 1 ⋅ 2 π − 2 1 ⋅ 2 1 ( sin x ) 2 ∣ 2 π 0 = π 4 − 1 4 = π − 1 4 =\frac{\pi }{4}-\frac{1}{4}=\frac{\pi -1}{4} = 4 π − 4 1 = 4 π − 1 F ( x ) = ∫ 0 π ln ( x 2 + 2 x cos t + 1 ) d t F(x)=\int_{0}^{\pi }\ln(x^2+2x\cos t +1)dt F ( x ) = ∫ 0 π ln ( x 2 + 2 x cos t + 1 ) d t F ( x ) = F ( − x ) F(x)=F(-x) F ( x ) = F ( − x ) F ( − x ) = ∫ 0 π ln ( x 2 − 2 x cos t + 1 ) d t F(-x)=\int_{0}^{\pi }\ln(x^2-2x\cos t +1)dt F ( − x ) = ∫ 0 π ln ( x 2 − 2 x cos t + 1 ) d t ∫ 0 π ln ( x 2 − 2 x cos t + 1 ) d t = ∫ 0 π ln ( x 2 + 2 x cos ( π − t ) + 1 ) d t \int_{0}^{\pi }\ln(x^2-2x\cos t +1)dt=\int_{0}^{\pi }\ln(x^2+2x\cos (\pi -t) +1)dt ∫ 0 π ln ( x 2 − 2 x cos t + 1 ) d t = ∫ 0 π ln ( x 2 + 2 x cos ( π − t ) + 1 ) d t = ∫ 0 π ln ( x 2 + 2 x cos t + 1 ) d t = F ( x ) =\int_{0}^{\pi }\ln(x^2+2x\cos t +1)dt=F(x) = ∫ 0 π ln ( x 2 + 2 x cos t + 1 ) d t = F ( x ) F ( x ) = F ( − x ) F(x)=F(-x) F ( x ) = F ( − x ) F ( x ) F(x) F ( x )
定积分的几何应用
x型图:由上下两个函数围成的面积(分上下观看)S = ∫ a b f 上 ( x ) − f 下 ( x ) d x S=\int_{a}^{b}f_上(x)-f_下(x)dx S = ∫ a b f 上 ( x ) − f 下 ( x ) d x
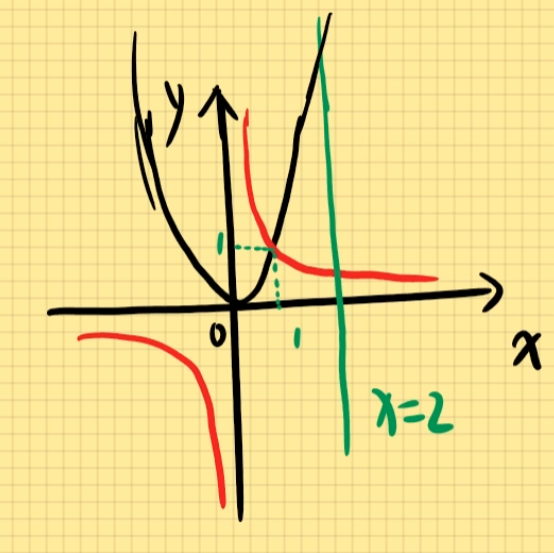
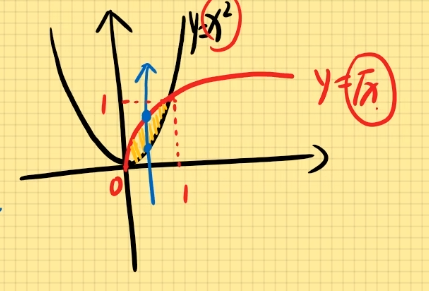
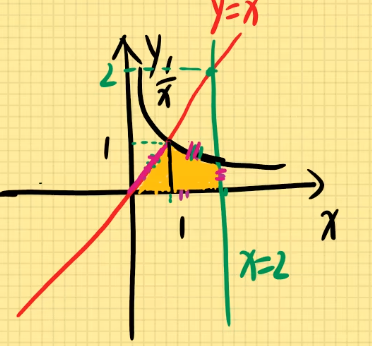
y型图:由左右两个函数围成的面积(分左右观看)S = ∫ c d f 右 ( y ) − f 左 ( y ) d x S=\int_{c}^{d}f_右(y)-f_左(y)dx S = ∫ c d f 右 ( y ) − f 左 ( y ) d x 选用y型图,改写为x=f(y) y = x 2 y=x^2 y = x 2 y = 1 x y=\frac{1}{x} y = x 1 x = 2 x=2 x = 2 S = ∫ 1 2 ( x 2 − 1 x ) d x S=\int_{1}^{2}(x^2-\frac{1}{x})dx S = ∫ 1 2 ( x 2 − x 1 ) d x = 1 3 x 3 − ln x ∣ 2 1 =\frac{1}{3}x^3-\ln x|\begin{matrix}2\\1\end{matrix} = 3 1 x 3 − ln x ∣ 2 1 = ( 8 3 − ln 2 ) − ( 1 3 − ln 1 ) =(\frac{8}{3}-\ln 2)-(\frac{1}{3}-\ln 1) = ( 3 8 − ln 2 ) − ( 3 1 − ln 1 ) = 7 3 − ln 2 =\frac{7}{3}-\ln 2 = 3 7 − ln 2 y = x 2 y=x^2 y = x 2 y = x y=\sqrt{x} y = x { y = x 2 y = x \left\{\begin{matrix}y=x^2\\y=\sqrt{x} \end{matrix}\right. { y = x 2 y = x x 2 = x x^2=\sqrt{x} x 2 = x ( 0 , 0 ) , ( 1 , 1 ) (0,0),(1,1) ( 0 , 0 ) , ( 1 , 1 ) S = ∫ 0 1 ( x − x 2 ) d x S=\int_{0}^{1}(\sqrt{x}-x^2)dx S = ∫ 0 1 ( x − x 2 ) d x ∫ 0 1 ( x 1 2 − x 2 ) d x \int_{0}^{1}(x^{\frac{1}{2} }-x^2)dx ∫ 0 1 ( x 2 1 − x 2 ) d x = 2 3 x 3 2 − 1 3 x 3 ∣ 1 0 =\frac{2}{3}x^{\frac{3}{2}}-\frac{1}{3}x^3|\begin{matrix}1\\0\end{matrix} = 3 2 x 2 3 − 3 1 x 3 ∣ 1 0 = 2 3 − 1 3 = 1 =\frac{2}{3}-\frac{1}{3}=1 = 3 2 − 3 1 = 1 S = ∫ 0 1 ( y − y 2 ) d y S=\int_{0}^{1}(\sqrt{y}-y^2)dy S = ∫ 0 1 ( y − y 2 ) d y = 2 3 y 3 2 − 1 3 y 3 ∣ 1 0 =\frac{2}{3}y^{\frac{3}{2}}-\frac{1}{3}y^3|\begin{matrix}1\\0\end{matrix} = 3 2 y 2 3 − 3 1 y 3 ∣ 1 0 = 2 3 − 1 3 = 1 3 =\frac{2}{3}-\frac{1}{3}=\frac{1}{3} = 3 2 − 3 1 = 3 1 y = 1 x y=\frac{1}{x} y = x 1 y = x y=x y = x x = 2 x=2 x = 2 x x x S = S 1 + S 2 S=S_1+S_2 S = S 1 + S 2 S 1 = ∫ 0 1 x d x = 1 2 ∣ 1 0 = 1 2 S_1=\int_{0}^{1}xdx=\frac{1}{2}|\begin{matrix}1\\0\end{matrix}=\frac{1}{2} S 1 = ∫ 0 1 x d x = 2 1 ∣ 1 0 = 2 1 S 2 = ∫ 1 2 1 x d x = ln ∣ x ∣ ∣ 2 1 = ln 2 S_2=\int_{1}^{2}\frac{1}{x}dx=\ln |x| |\begin{matrix}2\\1\end{matrix}=\ln 2 S 2 = ∫ 1 2 x 1 d x = ln ∣ x ∣ ∣ 2 1 = ln 2 S = S 1 + S 2 = ln 2 + 1 2 S=S_1+S_2=\ln 2+\frac{1}{2} S = S 1 + S 2 = ln 2 + 2 1
定积分求旋转体积
x型图绕x轴旋转V x = π ∫ a b f 2 ( x ) d x V_x=\pi \int_{a}^{b}f^2(x)dx V x = π ∫ a b f 2 ( x ) d x f 上 ( x ) , f 下 ( x ) f_上(x),f_下(x) f 上 ( x ) , f 下 ( x ) V x = π ∫ a b f 上 2 ( x ) − f 下 2 ( x ) d x V_x=\pi \int_{a}^{b}f_上^2(x)-f_下^2(x)dx V x = π ∫ a b f 上 2 ( x ) − f 下 2 ( x ) d x
y型图绕y轴旋转V y = π ∫ c d f 2 ( y ) d y V_y=\pi \int_{c}^{d}f^2(y)dy V y = π ∫ c d f 2 ( y ) d y f 左 ( y ) , f 右 ( y ) f_左(y),f_右(y) f 左 ( y ) , f 右 ( y ) V y = π ∫ a b f 右 2 ( y ) − f 左 2 ( y ) d y V_y=\pi \int_{a}^{b}f_右^2(y)-f_左^2(y)dy V y = π ∫ a b f 右 2 ( y ) − f 左 2 ( y ) d y
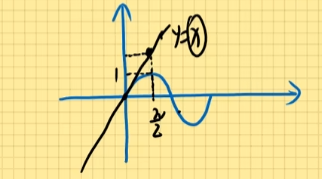
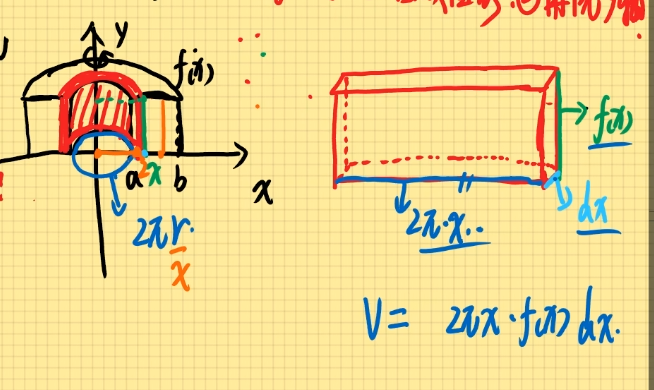
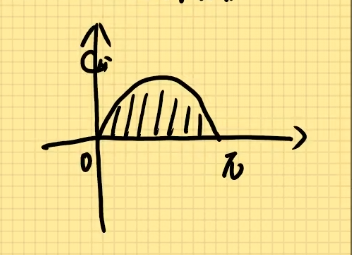
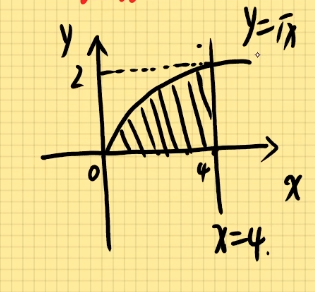
x型图绕y轴旋转V = 2 π ∫ a b x ⋅ f ( x ) d y V=2\pi \int_{a}^{b}x\cdot f(x)dy V = 2 π ∫ a b x ⋅ f ( x ) d y y = sin x , 0 ≤ x ≤ π y=\sin x,0\le x\le \pi y = sin x , 0 ≤ x ≤ π x x x V = 2 π ∫ a b x ⋅ f ( x ) d x V=2\pi \int_{a}^{b}x \cdot f(x)dx V = 2 π ∫ a b x ⋅ f ( x ) d x = 2 π ∫ 0 π x ⋅ sin x d x =2\pi \int_{0}^{\pi}x\cdot \sin xdx = 2 π ∫ 0 π x ⋅ sin x d x = − 2 π ∫ 0 π x d cos x =-2\pi \int_{0}^{\pi}x d\cos x = − 2 π ∫ 0 π x d cos x = − 2 π ( x ⋅ cos x ∣ π 0 − ∫ 0 π cos x d x ) =-2\pi (x\cdot \cos x|\begin{matrix}\pi\\0\end{matrix}-\int_{0}^{\pi}\cos xdx) = − 2 π ( x ⋅ cos x ∣ π 0 − ∫ 0 π cos x d x ) = − 2 π ( π ⋅ π − sin x ∣ π 0 ) =-2\pi (\pi \cdot \pi-\sin x|\begin{matrix}\pi\\0\end{matrix}) = − 2 π ( π ⋅ π − sin x ∣ π 0 ) = − 2 π ( π ⋅ ( − 1 ) − 0 =-2\pi (\pi \cdot (-1)-0 = − 2 π ( π ⋅ ( − 1 ) − 0 = 2 π 2 =2\pi ^2 = 2 π 2 y = x y=\sqrt{x} y = x x = 4 x=4 x = 4 S = ∫ 0 4 x d x S=\int_{0}^{4}\sqrt{x}dx S = ∫ 0 4 x d x = ∫ 0 4 x 1 2 d x =\int_{0}^{4}x^{\frac{1}{2} }dx = ∫ 0 4 x 2 1 d x = 2 3 ⋅ x 3 2 ∣ 4 0 =\frac{2}{3}\cdot x^{\frac{3}{2} }|\begin{matrix}4\\0\end{matrix} = 3 2 ⋅ x 2 3 ∣ 4 0 = 2 3 ⋅ ( 4 ) 3 2 =\frac{2}{3}\cdot (4)^{\frac{3}{2} } = 3 2 ⋅ ( 4 ) 2 3 = 16 3 =\frac{16}{3} = 3 1 6 V = π ∫ c d f 右 2 ( y ) − f 左 2 ( y ) d y V=\pi \int_{c}^{d}f_右^2(y)-f_左^2(y)dy V = π ∫ c d f 右 2 ( y ) − f 左 2 ( y ) d y = π ∫ 0 2 ( 4 2 − y 4 ) d y =\pi \int_{0}^{2}(4^2-y^4)dy = π ∫ 0 2 ( 4 2 − y 4 ) d y = π ∫ 0 2 16 − y 4 d y =\pi \int_{0}^{2}16-y^4dy = π ∫ 0 2 1 6 − y 4 d y = π ⋅ 1 ( 6 y − 1 5 x 5 ∣ 2 0 =\pi \cdot 1(6y-\frac{1}{5}x^5|\begin{matrix}2\\0\end{matrix} = π ⋅ 1 ( 6 y − 5 1 x 5 ∣ 2 0 = π ⋅ ( 32 − 32 5 ) =\pi \cdot (32-\frac{32}{5}) = π ⋅ ( 3 2 − 5 3 2 ) = 128 5 π =\frac{128}{5}\pi = 5 1 2 8 π V = 2 π ∫ a b x ⋅ f ( x ) d x V=2\pi \int_{a}^{b}x \cdot f(x)dx V = 2 π ∫ a b x ⋅ f ( x ) d x = 2 π ∫ 0 4 x ⋅ x d x =2\pi \int_{0}^{4}x\cdot \sqrt{x}dx = 2 π ∫ 0 4 x ⋅ x d x = 2 π ∫ 0 4 x 3 2 d x =2\pi \int_{0}^{4}x^{\frac{3}{2} }dx = 2 π ∫ 0 4 x 2 3 d x = 2 π 2 5 x 5 2 ∣ 4 0 =2\pi \frac{2}{5}x^{\frac{5}{2} }|\begin{matrix}4\\0\end{matrix} = 2 π 5 2 x 2 5 ∣ 4 0 = 4 π 5 4 2 5 =\frac{4\pi }{5} 4^{\frac{2}{5} } = 5 4 π 4 5 2 = 128 5 π =\frac{128}{5}\pi = 5 1 2 8 π







 例题2:求由函数与及x轴所围成的面积和绕y轴旋转一周所得旋转体积。
例题2:求由函数与及x轴所围成的面积和绕y轴旋转一周所得旋转体积。 或
或