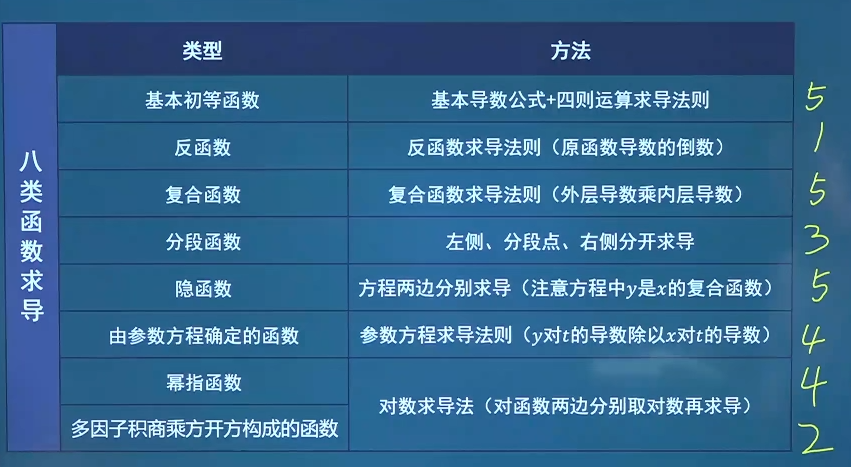
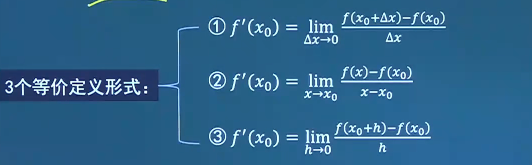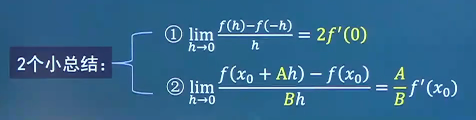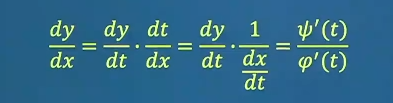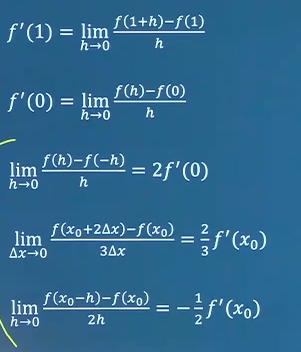一元函数微分学 导数 导数的定义 设函数y = f ( x ) y=f(x) y = f ( x ) x 0 x_0 x 0 x x x x 0 x_0 x 0 Δ x \Delta x Δ x x 0 + Δ x x_0+\Delta x x 0 + Δ x y y y Δ y = f ( x 0 + Δ x ) − f ( x 0 ) \Delta y=f(x_0+\Delta x)-f(x_0) Δ y = f ( x 0 + Δ x ) − f ( x 0 ) Δ y Δ x \frac{\Delta y}{\Delta x} Δ x Δ y Δ x → 0 \Delta x \to 0 Δ x → 0 y = f ( x ) y=f(x) y = f ( x ) x 0 x_0 x 0 y = f ( x ) y=f(x) y = f ( x ) x 0 x_0 x 0 f ′ ( x 0 ) = lim Δ x → 0 Δ y Δ x = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x f'(x_0)=\lim_{\Delta x \to 0}{\frac{\Delta y}{\Delta x} }=\lim_{\Delta x \to 0} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} f ′ ( x 0 ) = lim Δ x → 0 Δ x Δ y = lim Δ x → 0 Δ x f ( x 0 + Δ x ) − f ( x 0 ) y ′ ∣ x = x 0 ′ , d y d x ∣ x = x 0 ′ , d f ( x ) d x ∣ x = x 0 y'|_{x=x_{0'}},\frac{dy}{dx}|_{x=x_{0'}},\frac{df(x)}{dx}|_{x=x_0} y ′ ∣ x = x 0 ′ , d x d y ∣ x = x 0 ′ , d x d f ( x ) ∣ x = x 0
f ′ ( x 0 ) = lim Δ → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x f'(x_0)=\lim_{\Delta \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} f ′ ( x 0 ) = lim Δ → 0 Δ x f ( x 0 + Δ x ) − f ( x 0 ) f ′ ( x 0 ) = lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 f'(x_0)=\lim_{x \to x_0}\frac{f(x)-f(x_0)}{x-x_0} f ′ ( x 0 ) = lim x → x 0 x − x 0 f ( x ) − f ( x 0 ) f ′ ( x 0 ) = lim h → 0 f ( x 0 + h ) − f ( x 0 ) h f'(x_0)=\lim_{h \to 0}\frac{f(x_0+h)-f(x_0)}{h} f ′ ( x 0 ) = lim h → 0 h f ( x 0 + h ) − f ( x 0 ) f ′ ( x 0 ) = 1 , f ( x 0 ) = 0 f'(x_0)=1,f(x_0)=0 f ′ ( x 0 ) = 1 , f ( x 0 ) = 0 lim h → ∞ h f ( x 0 − 1 h ) \lim_{h \to \infty} hf(x_0-\frac{1}{h}) lim h → ∞ h f ( x 0 − h 1 ) __ -1__ .Δ x = 1 h \Delta x=\frac{1}{h} Δ x = h 1 lim Δ x → 0 f ( x 0 − Δ x ) − f ( x 0 ) Δ x = − f ′ ( x 0 ) = − 1 \lim_{\Delta x \to 0} \frac{f(x_0-\Delta x)-f(x_0)}{\Delta x}=-f'(x_0)=-1 lim Δ x → 0 Δ x f ( x 0 − Δ x ) − f ( x 0 ) = − f ′ ( x 0 ) = − 1 导函数的定义
结论
导数的定义 函数f ( x ) f(x) f ( x ) x 0 x_0 x 0
定义式:lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 = f ′ ( x 0 ) \lim_{x \to x_0} \frac{f(x)-f(x_0)}{x-x_0} =f'(x_0) lim x → x 0 x − x 0 f ( x ) − f ( x 0 ) = f ′ ( x 0 ) x − x 0 = Δ x x-x_0=\Delta x x − x 0 = Δ x
增量式:lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x = f ′ ( x 0 ) \lim_{\Delta x \to 0}{\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} }=f'(x_0) lim Δ x → 0 Δ x f ( x 0 + Δ x ) − f ( x 0 ) = f ′ ( x 0 )
Δ x \Delta x Δ x 整体思想:Δ x → □ \Delta x \to \Box Δ x → □
Δ x → 0 \Delta x \to 0 Δ x → 0 Δ x \Delta x Δ x
引申公式:lim Δ x → 0 f ( x 0 + a Δ x ) − f ( x 0 + b Δ x ) c Δ x = a − b c ⋅ f ′ ( x 0 ) \lim_{\Delta x \to 0}\frac{f(x_0+a\Delta x)-f(x_0+b\Delta x)}{c \Delta x}=\frac{a-b}{c}\cdot f'(x_0) lim Δ x → 0 c Δ x f ( x 0 + a Δ x ) − f ( x 0 + b Δ x ) = c a − b ⋅ f ′ ( x 0 ) lim Δ x → 0 f ( x 0 + a Δ x ) − f ( x 0 + b Δ x ) c Δ x \lim_{\Delta x \to 0}\frac{f(x_0+a\Delta x)-f(x_0+b\Delta x)}{c \Delta x} lim Δ x → 0 c Δ x f ( x 0 + a Δ x ) − f ( x 0 + b Δ x ) ( x 0 + a Δ x ) − ( x 0 + b Δ x ) c Δ x = ( a − b ) Δ x c Δ x ⋅ f ′ ( x 0 ) \frac{(x_0+a \Delta x )-(x_0+b \Delta x)}{c \Delta x}=\frac{(a-b)\Delta x}{c\Delta x}\cdot f'(x_0) c Δ x ( x 0 + a Δ x ) − ( x 0 + b Δ x ) = c Δ x ( a − b ) Δ x ⋅ f ′ ( x 0 )
已知f ( x ) f(x) f ( x ) x = x 0 x=x_0 x = x 0 lim h → 0 ] f ( x 0 + h ) − f ( x 0 ) h = \lim_{h \to 0}]\frac{f(x_0+h)-f(x_0)}{h}= lim h → 0 ] h f ( x 0 + h ) − f ( x 0 ) = f ′ ( x 0 ) f'(x_0) f ′ ( x 0 ) h → 0 ; ∴ h = Δ x h \to 0;\therefore h=\Delta x h → 0 ; ∴ h = Δ x lim Δ x → 0 ] f ( x 0 + Δ x ) − f ( x 0 ) Δ x = f ′ ( x 0 ) \lim_{\Delta x \to 0}]\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=f'(x_0) lim Δ x → 0 ] Δ x f ( x 0 + Δ x ) − f ( x 0 ) = f ′ ( x 0 )
设f ( x ) f(x) f ( x ) x = a x=a x = a lim Δ x → 0 f ( a + Δ x ) − f ( a − Δ x ) Δ x = \lim_{\Delta x \to 0}\frac{f(a+\Delta x)-f(a-\Delta x)}{\Delta x}= lim Δ x → 0 Δ x f ( a + Δ x ) − f ( a − Δ x ) = 2 f ′ ( a ) 2f'(a) 2 f ′ ( a ) 1 − ( − 1 ) 1 ⋅ f ( a ) = 2 f ′ ( a ) \frac{1-(-1)}{1} \cdot f(a)=2f'(a) 1 1 − ( − 1 ) ⋅ f ( a ) = 2 f ′ ( a ) ( a + Δ x ) − ( a − Δ x ) Δ x ⋅ f ′ ( a ) = 2 Δ x Δ x = 2 f ′ ( a ) \frac{(a+\Delta x)-(a-\Delta x)}{\Delta x}\cdot f'(a)=\frac{2\Delta x}{\Delta x}=2f'(a) Δ x ( a + Δ x ) − ( a − Δ x ) ⋅ f ′ ( a ) = Δ x 2 Δ x = 2 f ′ ( a )
设f ′ ( 0 ) = a f'(0)=a f ′ ( 0 ) = a lim Δ x → 0 f ( − Δ x ) − f ( 0 ) Δ x = \lim_{\Delta x \to 0}\frac{f(-\Delta x)-f(0)}{\Delta x}= lim Δ x → 0 Δ x f ( − Δ x ) − f ( 0 ) = _ − a -a − a __ ;− Δ x − 0 Δ x ⋅ f ′ ( 0 ) = − f ′ ( 0 ) = − a \frac{-\Delta x-0}{\Delta x} \cdot f'(0)=-f'(0)=-a Δ x − Δ x − 0 ⋅ f ′ ( 0 ) = − f ′ ( 0 ) = − a
设f ′ ( x 0 ) = − 1 f'(x_0)=-1 f ′ ( x 0 ) = − 1 lim x → 0 x f ( x 0 − 2 x ) − f ( x 0 − x ) = \lim_{x \to 0}\frac{x}{f(x_0-2x)-f(x_0-x)}= lim x → 0 f ( x 0 − 2 x ) − f ( x 0 − x ) x = lim Δ x → 0 Δ x f ( x 0 − 2 Δ x ) − f ( x 0 − Δ x ) \lim_{\Delta x \to 0}\frac{\Delta x}{f(x_0-2\Delta x)-f(x_0-\Delta x)} lim Δ x → 0 f ( x 0 − 2 Δ x ) − f ( x 0 − Δ x ) Δ x lim Δ x → 0 1 f ( x 0 − 2 Δ x ) − f ( x 0 − Δ x ) Δ x \lim_{\Delta x \to 0}\frac{1}{\frac{f(x_0-2\Delta x)-f(x_0-\Delta x)}{\Delta x}} lim Δ x → 0 Δ x f ( x 0 − 2 Δ x ) − f ( x 0 − Δ x ) 1 lim Δ x → 0 1 − 2 − ( − 1 ) 1 ⋅ f ′ ( x 0 ) = 1 \lim_{\Delta x \to 0}\frac{1}{\frac{-2-(-1)}{1}\cdot f'(x_0)}=1 lim Δ x → 0 1 − 2 − ( − 1 ) ⋅ f ′ ( x 0 ) 1 = 1
导数定义,求函数f ( x ) f(x) f ( x ) 特点:此时的f ( x ) f(x) f ( x )
已知f ( x ) f(x) f ( x ) 解法:根据导数定义,凑出相关极限f ( x ) f(x) f ( x ) R R R f ( 0 ) = 0 f(0)=0 f ( 0 ) = 0 f ′ ( 0 ) = 2 f'(0)=2 f ′ ( 0 ) = 2 lim x → 0 f ( e x − 1 ) x \lim_{x \to 0}\frac{f(e^x-1)}{x} lim x → 0 x f ( e x − 1 ) ∵ f ( 0 ) = lim x → 0 f ( x ) − f ( 0 ) x − 0 = lim x → 0 f ( x ) x = 2 \because f(0)=\lim_{x \to 0} \frac{f(x)-f(0)}{x-0}=\lim_{x \to 0} \frac{f(x)}{x}=2 ∵ f ( 0 ) = lim x → 0 x − 0 f ( x ) − f ( 0 ) = lim x → 0 x f ( x ) = 2 ∴ lim x → 0 f ( e x ) − 1 x = lim x → 0 f ( e x ) − f ( 0 ) ( e x − 1 ) − 0 ⋅ e x − 1 x = lim x → 0 2 ⋅ e x − 1 x = 2 \therefore \lim_{x \to 0} \frac{f(e^x)-1}{x}=\lim_{x \to 0} \frac{f(e^x)-f(0)}{(e^x-1)-0} \cdot \frac{e^x-1}{x}=\lim_{x \to 0} 2\cdot \frac{e^x-1}{x}=2 ∴ lim x → 0 x f ( e x ) − 1 = lim x → 0 ( e x − 1 ) − 0 f ( e x ) − f ( 0 ) ⋅ x e x − 1 = lim x → 0 2 ⋅ x e x − 1 = 2 f ( x ) f(x) f ( x ) x = 0 x=0 x = 0 f ( 0 ) = 0 f(0)=0 f ( 0 ) = 0 f ′ ( 0 ) = 2 f'(0)=2 f ′ ( 0 ) = 2 lim x → 0 f ( ) 1 − cos x tan x 2 \lim_{x \to 0}\frac{f()1-\cos x}{\tan x^2} lim x → 0 t a n x 2 f ( ) 1 − c o s x ∵ lim x → 0 f ( x ) x = 2 \because \lim_{x \to 0} \frac{f(x)}{x}=2 ∵ lim x → 0 x f ( x ) = 2 ∴ lim x → 0 f ( 1 − cos x ) tan x 2 = lim x → 0 1 − cos x x 2 = lim x → 0 f ( 1 − cos x ) x − cos x ⋅ 1 − cos x x 2 = lim x → 0 2 ⋅ 1 2 x 2 x 2 = 1 \therefore \lim_{x \to 0} \frac{f(1-\cos x)}{\tan x^2}=\lim_{x \to 0} \frac{1-\cos x}{x^2} =\lim_{x \to 0} \frac{f(1-\cos x) }{x-\cos x } \cdot \frac{1-\cos x}{x^2} =\lim_{x \to 0} 2 \cdot \frac{\frac{1}{2}x^2 }{x^2} =1 ∴ lim x → 0 t a n x 2 f ( 1 − c o s x ) = lim x → 0 x 2 1 − c o s x = lim x → 0 x − c o s x f ( 1 − c o s x ) ⋅ x 2 1 − c o s x = lim x → 0 2 ⋅ x 2 2 1 x 2 = 1
已知函数极限,求相关导数 已知f ( x ) f(x) f ( x ) x = a x=a x = a lim x → a f ( x ) x − a = 2 \lim_{x \to a}\frac{f(x)}{x-a}=2 lim x → a x − a f ( x ) = 2 f ′ ( a ) f'(a) f ′ ( a ) f ( a ) f(a) f ( a ) ∵ lim x → 0 f ( x ) x − a = 2 \because \lim_{x \to 0} \frac{f(x)}{x-a} =2 ∵ lim x → 0 x − a f ( x ) = 2 ∴ lim x → 0 f ( x ) = f ( a ) = 0 \therefore \lim_{x \to 0} f(x)=f(a)=0 ∴ lim x → 0 f ( x ) = f ( a ) = 0 f ′ ( a ) = lim x → a f ( x ) − f ( a ) x − a = lim x → a f ( x ) x − a = 2 f'(a)=\lim_{x \to a} \frac{f(x)-f(a)}{x-a}=\lim_{x \to a} \frac{f(x)}{x-a}=2 f ′ ( a ) = lim x → a x − a f ( x ) − f ( a ) = lim x → a x − a f ( x ) = 2
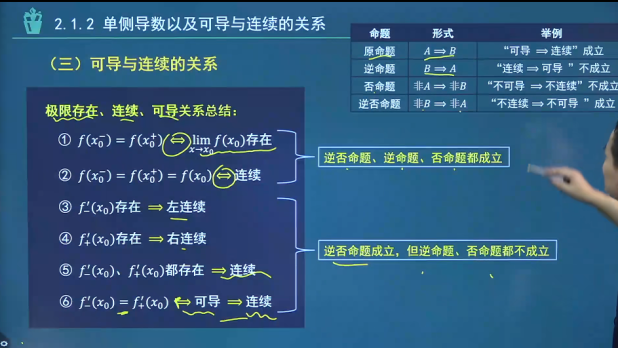
左导数与右导数 左、右导数定义 左导数和右导数统称单侧函数f − ′ ( x ) = lim x → x 0 − f ( x ) − f ( x 0 ) x − x 0 f_-'(x)=\lim_{x \to x_0^-}\frac{f(x)-f(x_0)}{x-x_0} f − ′ ( x ) = lim x → x 0 − x − x 0 f ( x ) − f ( x 0 ) f + ′ ( x ) = lim x → x 0 + f ( x ) − f ( x 0 ) x − x 0 f_+'(x)=\lim_{x \to x_0^+}\frac{f(x)-f(x_0)}{x-x_0} f + ′ ( x ) = lim x → x 0 + x − x 0 f ( x ) − f ( x 0 )
函数在某点x 0 x_0 x 0 f − ′ ( x 0 ) = f + ′ ( x 0 ) f_-'(x_0)=f_+'(x_0) f − ′ ( x 0 ) = f + ′ ( x 0 )
可导的必要条件:可导函数必连续;
题型:
告知f ( x ) f(x) f ( x )
可导→ \to → → \to → f ( x ) = { e x . x > 0 sin a x + b . x ≤ 0 f(x)=\left\{\begin{matrix}e^x.x>0 \\ \sin ax+b.x\le 0 \end{matrix}\right. f ( x ) = { e x . x > 0 sin a x + b . x ≤ 0 x = 0 x=0 x = 0 a , b a,b a , b ∵ f ( x ) \because f(x) ∵ f ( x ) x = 0 x=0 x = 0 f ( x ) f(x) f ( x ) x = 0 x=0 x = 0 x = o , f ( 0 ) = b x=o,f(0)=b x = o , f ( 0 ) = b lim x → 0 − f ( x ) = lim x → 0 − ( sin a x + b ) = b \lim_{x \to 0^-}f(x)=\lim_{x \to 0^-}(\sin ax+b)=b lim x → 0 − f ( x ) = lim x → 0 − ( sin a x + b ) = b lim x → 0 + f ( x ) = lim x → 0 + e x = 1 \lim_{x \to 0^+}f(x)=\lim_{x \to 0^+}e^x =1 lim x → 0 + f ( x ) = lim x → 0 + e x = 1 → \to → b = 1 b=1 b = 1 f − ′ ( 0 ) = f + ′ ( 0 ) f_-'(0)=f_+'(0) f − ′ ( 0 ) = f + ′ ( 0 ) f − ′ ( 0 ) = lim x → 0 − f ( x ) − f ( 0 ) x − 0 = lim x → 0 − sin a x + 1 − 1 x = a f_-'(0)=\lim_{x \to 0^-}\frac{f(x)-f(0)}{x-0}=\lim_{x \to 0^-}\frac{\sin ax+1-1}{x}=a f − ′ ( 0 ) = lim x → 0 − x − 0 f ( x ) − f ( 0 ) = lim x → 0 − x s i n a x + 1 − 1 = a f + ′ ( 0 ) = lim x → 0 + f ( x ) − f ( 0 ) x − 0 = lim x → 0 + e x − 1 x = 1 f_+'(0)=\lim_{x \to 0^+}\frac{f(x)-f(0)}{x-0}=\lim_{x \to 0^+}\frac{e^x-1}{x}=1 f + ′ ( 0 ) = lim x → 0 + x − 0 f ( x ) − f ( 0 ) = lim x → 0 + x e x − 1 = 1 → \to → a = 1 a=1 a = 1 a = 1 , b = 1 a=1,b=1 a = 1 , b = 1 f ( x ) = { l n ( 1 + x 2 ) x , x > 0 a x + b , x ≤ 0 f(x)=\left\{\begin{matrix} \frac{ln(1+x^2)}{x},x>0 \\ ax+b, x\le 0 \end{matrix}\right. f ( x ) = { x l n ( 1 + x 2 ) , x > 0 a x + b , x ≤ 0 x = 0 x=0 x = 0 a , b a,b a , b ∵ f ( x ) \because f(x) ∵ f ( x ) x = 0 x=0 x = 0 f ( x ) f(x) f ( x ) x = 0 x=0 x = 0 x = 0 , f ( 0 ) = b x=0,f(0)=b x = 0 , f ( 0 ) = b lim x → 0 − f ( x ) = lim x → 0 − ( sin a x + b ) = b \lim_{x \to 0^-}f(x)=\lim_{x \to 0^-}(\sin ax+b)=b lim x → 0 − f ( x ) = lim x → 0 − ( sin a x + b ) = b lim x → 0 + f ( x ) = lim x → 0 + l n ( 1 + x 2 ) x = lim x → 0 + x 2 x = lim x → 0 + x = 0 \lim_{x \to 0^+}f(x)=\lim_{x \to 0^+}\frac{ln(1+x^2)}{x} =\lim_{x \to 0^+}\frac{x^2}{x}=\lim_{x \to 0^+}x=0 lim x → 0 + f ( x ) = lim x → 0 + x l n ( 1 + x 2 ) = lim x → 0 + x x 2 = lim x → 0 + x = 0 → \to → b = 0 b=0 b = 0 f − ′ ( 0 ) = f + ′ ( 0 ) f_-'(0)=f_+'(0) f − ′ ( 0 ) = f + ′ ( 0 ) f − ′ ( 0 ) = lim x → 0 − f ( x ) − f ( 0 ) x − 0 = lim x → 0 − sin a x x = a f_-'(0)=\lim_{x \to 0^-}\frac{f(x)-f(0)}{x-0}=\lim_{x \to 0^-}\frac{\sin ax}{x}=a f − ′ ( 0 ) = lim x → 0 − x − 0 f ( x ) − f ( 0 ) = lim x → 0 − x s i n a x = a f + ′ ( 0 ) = lim x → 0 + f ( x ) − f ( 0 ) x − 0 = lim x → 0 + l n ( 1 + x 2 ) x 2 = lim x → 0 + x 2 x 2 = 1 f_+'(0)=\lim_{x \to 0^+}\frac{f(x)-f(0)}{x-0}=\lim_{x \to 0^+}\frac{ln(1+x^2)}{x^2}=\lim_{x \to 0^+}\frac{x^2}{x^2}=1 f + ′ ( 0 ) = lim x → 0 + x − 0 f ( x ) − f ( 0 ) = lim x → 0 + x 2 l n ( 1 + x 2 ) = lim x → 0 + x 2 x 2 = 1 → \to → a = 1 a=1 a = 1 a = 1 , b = 0 a=1,b=0 a = 1 , b = 0
可导与连续的关系
基本导数公式和四则运算求导法则
函数的求导方法 1.复合函数求导外层求导,再乘以内层求导。 y = l n cos x ,求 y ′ y=ln \cos x, 求y' y = l n cos x , 求 y ′ y ′ = 1 cos x ⋅ ( − sin x ) y'=\frac{1}{\cos x}\cdot (- \sin x) y ′ = c o s x 1 ⋅ ( − sin x ) − tan x - \tan x − tan x f ( x ) f(x) f ( x ) y = f ( 1 x 3 ) y=f(\frac{1}{x^3}) y = f ( x 3 1 ) f ′ ( 1 x 3 ) ⋅ ( − 3 1 x 4 ) f'(\frac{1}{x^3}) \cdot (-3 \frac{1}{x^4}) f ′ ( x 3 1 ) ⋅ ( − 3 x 4 1 ) − 3 f ′ ( 1 x 3 ) x 4 \frac{-3f'(\frac{1}{x^3})}{x^4} x 4 − 3 f ′ ( x 3 1 ) 分段点两边分别求,中间分段点单独求 y 是 x y是x y 是 x e y + x y − e = 0 e^y+xy-e=0 e y + x y − e = 0 y ′ y' y ′ y = f ( x ) y=f(x) y = f ( x ) e y y ′ + y + x y ′ − 0 = 0 e^yy'+y+xy'-0=0 e y y ′ + y + x y ′ − 0 = 0 y ′ = − y e y + x y'=\frac{-y}{e^y+x} y ′ = e y + x − y 3 x y + l n y = 1 3xy+lny=1 3 x y + l n y = 1 x = 0 x=0 x = 0 d y d x ∣ x = 0 \frac{dy}{dx}|_{x=0} d x d y ∣ x = 0 3 y + 3 x ⋅ y ′ + y ′ y = 0 3y+3x \cdot y'+\frac{y'}{y}=0 3 y + 3 x ⋅ y ′ + y y ′ = 0 y ′ = − 3 y 3 x + 1 y = − 3 y 2 3 x y + 1 y'=\frac{-3y}{3x+\frac{1}{y}}=\frac{-3y^2}{3xy+1} y ′ = 3 x + y 1 − 3 y = 3 x y + 1 − 3 y 2 x = 0 时, y = e x=0时,y=e x = 0 时 , y = e d y d x ∣ x = 0 = − 3 e 2 0 + 1 = − 3 e 2 \frac{dy}{dx}|_{x=0}=\frac{-3e^2}{0+1}=-3e^2 d x d y ∣ x = 0 = 0 + 1 − 3 e 2 = − 3 e 2 y = f ( x ) y=f(x) y = f ( x ) arcsin y = e x \arcsin y=e^x arcsin y = e x y ′ y' y ′ arcsin x = 1 1 − x 2 \arcsin x= \frac{1}{ \sqrt{1-x^2} } arcsin x = 1 − x 2 1 1 1 − y 2 y ′ = e x \frac{1}{ \sqrt{1-y^2} } y'=e^x 1 − y 2 1 y ′ = e x y ′ = e x 1 − y 2 y'=e^x\sqrt{1-y^2} y ′ = e x 1 − y 2 y = y ( x ) y=y(x) y = y ( x ) { x = 3 t 2 − 1 y = e 2 t + 1 \left\{\begin{matrix}x=3t^2-1
\\
y=e^{2t}+1
\end{matrix}\right. { x = 3 t 2 − 1 y = e 2 t + 1 d y d x \frac{dy}{dx} d x d y d y d t = 2 e 2 t \frac{dy}{dt}=2e^{2t} d t d y = 2 e 2 t d x d t = 6 t \frac{dx}{dt}=6t d t d x = 6 t d y d x = 2 e 2 t 6 t = e 2 t 3 t \frac{dy}{dx}=\frac{2e^{2t} }{6t}=\frac{ e^{2t} }{3t} d x d y = 6 t 2 e 2 t = 3 t e 2 t { x = t − 1 t y = 1 2 t 2 + l n t \left\{\begin{matrix}
x=t-\frac{1}{t}
\\
y=\frac{1}{2}t^2+lnt
\end{matrix}\right. { x = t − t 1 y = 2 1 t 2 + l n t d y d x ∣ t = 1 \frac{dy}{dx}|_{t=1} d x d y ∣ t = 1 d y d t = t + 1 t \frac{dy}{dt}=t+\frac{1}{t} d t d y = t + t 1 d x d t = 1 + 1 t 2 \frac{dx}{dt}=1+\frac{1}{t^2} d t d x = 1 + t 2 1 d y d x = t + 1 t 1 + 1 t 2 \frac{dy}{dx}=\frac{t+\frac{1}{t} }{1+\frac{1}{t^2} } d x d y = 1 + t 2 1 t + t 1 y = x x ( x > 0 ) y=x^x(x>0) y = x x ( x > 0 ) l n y = l n x x = x l n x lny=lnx^x=xlnx l n y = l n x x = x l n x y ′ y = l n x + x ⋅ 1 x \frac{y'}{y}=lnx+x \cdot \frac{1}{x} y y ′ = l n x + x ⋅ x 1 y ′ = y ( l n x + 1 ) y'=y(lnx+1) y ′ = y ( l n x + 1 ) x x ( l n x + 1 ) x^x(lnx+1) x x ( l n x + 1 ) y = x sin x ( x > 0 ) y=x^{\sin x}(x>0) y = x s i n x ( x > 0 ) l n y = sin x ⋅ l n x lny=\sin x \cdot lnx l n y = sin x ⋅ l n x y ′ y = cos x ⋅ l n x + sin x ⋅ 1 x \frac{y'}{y}=\cos x \cdot lnx+\sin x \cdot \frac{1}{x} y y ′ = cos x ⋅ l n x + sin x ⋅ x 1 y ′ = x sin x ( cos x ⋅ l n x + sin x x ) y'=x^{\sin x}(\cos x \cdot lnx+\frac{\sin x}{x}) y ′ = x s i n x ( cos x ⋅ l n x + x s i n x ) y = ( 1 + 2 x ) cos x ( x > − 1 2 ) y=(1+2x)^{\cos x}(x>-\frac{1}{2}) y = ( 1 + 2 x ) c o s x ( x > − 2 1 ) l n y = cos x ⋅ l n ( 1 + 2 x ) lny=\cos x \cdot ln(1+2x) l n y = cos x ⋅ l n ( 1 + 2 x ) y ′ y = − sin x ⋅ l n ( 1 + 2 x ) + cos x ⋅ 2 1 + 2 x \frac{y'}{y}=-\sin x \cdot ln(1+2x)+\cos x \cdot \frac{2}{1+2x} y y ′ = − sin x ⋅ l n ( 1 + 2 x ) + cos x ⋅ 1 + 2 x 2 y ′ = ( 1 + 2 x ) cos x ( 2 ⋅ cos x 1 + 2 x − sin x ⋅ l n ( 1 + 2 x ) ) y'=(1+2x)^{\cos x}(\frac{2 \cdot \cos x}{1+2x}-\sin x \cdot ln(1+2x) ) y ′ = ( 1 + 2 x ) c o s x ( 1 + 2 x 2 ⋅ c o s x − sin x ⋅ l n ( 1 + 2 x ) ) ( x − 1 ) ( x − 2 ) ( x − 3 ) ( x − 4 ) \sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)} } ( x − 3 ) ( x − 4 ) ( x − 1 ) ( x − 2 ) l n y = l n ( ( x − 1 ) ( x − 2 ) ( x − 3 ) ( x − 4 ) ) 1 2 = 1 2 l n ( x − 1 ) ( x − 2 ) ( x − 3 ) ( x − 4 ) lny=ln(\frac{(x-1)(x-2)}{(x-3)(x-4)} )^\frac{1}{2}=\frac{1}{2} ln\frac{(x-1)(x-2)}{(x-3)(x-4)} l n y = l n ( ( x − 3 ) ( x − 4 ) ( x − 1 ) ( x − 2 ) ) 2 1 = 2 1 l n ( x − 3 ) ( x − 4 ) ( x − 1 ) ( x − 2 ) 1 2 ( l n ( x − 1 ) + l n ( x − 2 ) − l n ( x − 3 ) − l n ( x − 4 ) ) \frac{1}{2}(ln(x-1)+ln(x-2)-ln(x-3)-ln(x-4) ) 2 1 ( l n ( x − 1 ) + l n ( x − 2 ) − l n ( x − 3 ) − l n ( x − 4 ) ) 2 y ′ y = 1 x − 1 + 1 x − 2 − 1 x − 3 − 1 x − 4 2\frac{y'}{y}=\frac{1}{x-1}+\frac{1}{x-2}-\frac{1}{x-3}-\frac{1}{x-4} 2 y y ′ = x − 1 1 + x − 2 1 − x − 3 1 − x − 4 1 y ′ = y 2 ( 1 x − 1 + 1 x − 2 − 1 x − 3 − 1 x − 4 ) y'=\frac{y}{2}(\frac{1}{x-1}+\frac{1}{x-2}-\frac{1}{x-3}-\frac{1}{x-4}) y ′ = 2 y ( x − 1 1 + x − 2 1 − x − 3 1 − x − 4 1 ) 例题2
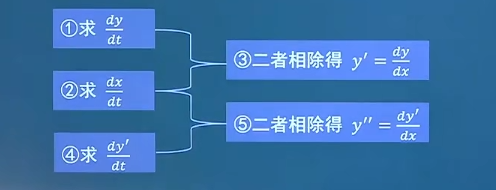
高阶导数 1.定义y = f ( x ) y=f(x) y = f ( x ) y ′ y' y ′ y ′ y' y ′ y ′ ′ y'' y ′ ′ y ( 4 ) y^{(4)} y ( 4 ) y ( n − 1 ) y^{(n-1)} y ( n − 1 ) y ( n ) y^{(n)} y ( n ) f ( n ) ( x ) , d n y d x n , d n f ( x ) d x n f^{(n)}(x),\frac{d^ny}{dx^n},\frac{d^nf(x)}{dx^n} f ( n ) ( x ) , d x n d n y , d x n d n f ( x ) y = 2 x 4 − x 2 + e x y=2x^4-x^2+e^x y = 2 x 4 − x 2 + e x y ′ = 8 x 3 − 2 x + e x y'=8x^3-2x+e^x y ′ = 8 x 3 − 2 x + e x y ′ ′ = 24 x 2 − 2 + e x y''=24x^2-2+e^x y ′ ′ = 2 4 x 2 − 2 + e x y ′ ′ ′ = 48 x + e x y'''=48x+e^x y ′ ′ ′ = 4 8 x + e x y = l n ( sin x ) y=ln(\sin x) y = l n ( sin x ) = 1 sin x ⋅ cos x = cot x = y ′ ′ = − csc 2 x =\frac{1}{\sin x}\cdot \cos x=\cot x
=y''=-\csc^2x = s i n x 1 ⋅ cos x = cot x = y ′ ′ = − csc 2 x x 2 + y 2 = 1 x^2+y^2=1 x 2 + y 2 = 1 = 2 x + 2 y ⋅ y ′ = 0 = y ′ = − x y = y ′ ′ = − y − y ′ x y 2 = − y + x y ⋅ x y 2 = − 1 y 3 =2x+2y \cdot y'=0
=y'=-\frac{x}{y}
=y''=-\frac{y-y'x}{y^2}=-\frac{y+\frac{x}{y} \cdot x }{y^2}
=-\frac{1}{y^3} = 2 x + 2 y ⋅ y ′ = 0 = y ′ = − y x = y ′ ′ = − y 2 y − y ′ x = − y 2 y + y x ⋅ x = − y 3 1 常用高阶求导公式 y = x 2000 + e x + cos x y=x^{2000}+e^x+\cos x y = x 2 0 0 0 + e x + cos x y ( 2025 ) = e x − sin x y^{(2025)}=e^x-\sin x y ( 2 0 2 5 ) = e x − sin x 求导方法 y = y ( x ) y=y(x) y = y ( x ) { x = 1 2 t 2 − 1 y = x t + 1 \left\{\begin{matrix}
x=\frac{1}{2}t^2-1
\\
y=x^t+1
\end{matrix}\right. { x = 2 1 t 2 − 1 y = x t + 1 d 2 y d x 2 \frac{d^2y}{dx^2} d x 2 d 2 y = d y d t = e t = d x d t = t = d y d x = e t t = d y ′ d t = ( e t t ) ′ = e t ⋅ t − e t t 2 = d 2 y d x 2 = e t ⋅ t − e t t 3 =\frac{dy}{dt}=e^t
=\frac{dx}{dt}=t
=\frac{dy}{dx}=\frac{e^t}{t}
=\frac{dy'}{dt}=(\frac{e^t}{t})'=\frac{e^t \cdot t-e^t}{t^2}
=\frac{d^2y}{dx^2}=\frac{e^t \cdot t-e^t}{t^3} = d t d y = e t = d t d x = t = d x d y = t e t = d t d y ′ = ( t e t ) ′ = t 2 e t ⋅ t − e t = d x 2 d 2 y = t 3 e t ⋅ t − e t { x = t − 1 t y = 1 2 t 2 + l n t \left\{\begin{matrix}
x=t-\frac{1}{t}
\\
y=\frac{1}{2}t^2+lnt
\end{matrix}\right. { x = t − t 1 y = 2 1 t 2 + l n t d 2 y d x 2 \frac{d^2y}{dx^2} d x 2 d 2 y = d y d t = t + 1 t = d x d t = 1 + 1 t 2 = y ′ = d y d x = t + 1 t 1 + 1 t 2 = t = d y ′ d t = 1 = d 2 y d x 2 = t 2 t 2 + 1 =\frac{dy}{dt}=t+\frac{1}{t}
=\frac{dx}{dt}=1+\frac{1}{t^2}
=y'=\frac{dy}{dx}=\frac{t+\frac{1}{t} }{1+\frac{1}{t^2} }=t
=\frac{dy'}{dt}=1
=\frac{d^2y}{dx^2}=\frac{t^2}{t^2+1} = d t d y = t + t 1 = d t d x = 1 + t 2 1 = y ′ = d x d y = 1 + t 2 1 t + t 1 = t = d t d y ′ = 1 = d x 2 d 2 y = t 2 + 1 t 2
导数的习题
设f ′ ( x 0 ) f'(x_0) f ′ ( x 0 ) lim Δ x → 0 f ( x 0 − 1 2 Δ x ) − f ( x 0 ) − Δ x = − 1 2 ÷ − 1 = 1 2 f ′ ( x 0 ) \lim_{\Delta x \to 0} \frac{f(x_0-\frac{1}{2}\Delta x )-f(x_0)}{-\Delta x}=-\frac{1}{2} {\div} -1=\frac{1}{2}f'(x_0) lim Δ x → 0 − Δ x f ( x 0 − 2 1 Δ x ) − f ( x 0 ) = − 2 1 ÷ − 1 = 2 1 f ′ ( x 0 )
求函数y = f ( cos 2 x ) y=f(\cos 2x) y = f ( cos 2 x ) y ′ = f ′ ( cos 2 x ) ⋅ ( − sin 2 x ) ⋅ 2 = − 2 sin 2 x f ′ ( cos 2 x ) y'=f'(\cos 2x) \cdot (-\sin 2x) \cdot 2
=-2 \sin 2x f'(\cos 2x)
y ′ = f ′ ( cos 2 x ) ⋅ ( − sin 2 x ) ⋅ 2 = − 2 sin 2 x f ′ ( cos 2 x )
求函数y = x + 1 − x − 1 x + 1 + x − 1 y=\frac{\sqrt{x+1}-\sqrt{x-1} }{\sqrt{x+1}+\sqrt{x-1} } y = x + 1 + x − 1 x + 1 − x − 1 y = ( x + 1 − x − 1 ) 2 ( x + 1 + x − 1 ) ( x + 1 − x − 1 ) = 2 x − 2 x 2 − 1 2 = x − x 2 − 1 = y ′ = 1 − 1 2 ( x 2 − 1 ) − 1 2 ⋅ 2 x = 1 − x x 2 − 1 y=\frac{(\sqrt{x+1}-\sqrt{x-1} )^2}{(\sqrt{x+1}+\sqrt{x-1})(\sqrt{x+1}-\sqrt{x-1} ) }
=\frac{2x-2\sqrt{x^2-1} }{2}=x-\sqrt{x^2-1}
=y'=1-\frac{1}{2}(x^2-1)^{-\frac{1}{2}} \cdot 2x
=1-\frac{x}{\sqrt{x^2-1} }
y = ( x + 1 + x − 1 ) ( x + 1 − x − 1 ) ( x + 1 − x − 1 ) 2 = 2 2 x − 2 x 2 − 1 = x − x 2 − 1 = y ′ = 1 − 2 1 ( x 2 − 1 ) − 2 1 ⋅ 2 x = 1 − x 2 − 1 x
求由方程x y = e x + y xy=e^{x+y} x y = e x + y y + x y ′ = e x + y ( 1 + y ′ ) = y + x y ′ = e x + y + e x + y y ′ = y ′ = e x + y − y x − e x + y y+xy'=e^{x+y}(1+y')
=y+xy'=e^{x+y}+e^{x+y}y'
=y'=\frac{e^{x+y}-y}{x-e^{x+y} }
y + x y ′ = e x + y ( 1 + y ′ ) = y + x y ′ = e x + y + e x + y y ′ = y ′ = x − e x + y e x + y − y
已知{ x = e t sin t y = e t cos t \left\{\begin{matrix}
x=e^t \sin t
\\
y=e^t \cos t
\end{matrix}\right. { x = e t sin t y = e t cos t t = π 3 时 d y d x 的值 t=\frac{\pi}{3}时\frac{dy}{dx}的值 t = 3 π 时 d x d y 的 值 d y d t = ( cos t − sin t ) e t = d x d t = e t ( cos t + sin t ) = d y d x = cos t − sin t cos t + sin t = d y d x ∣ t = π 3 = 1 2 − 3 2 1 2 + 3 2 = 3 − 2 \frac{dy}{dt}=(\cos t-\sin t)e^t
=\frac{dx}{dt}=e^t(\cos t+\sin t)
=\frac{dy}{dx}=\frac{\cos t-\sin t}{\cos t+\sin t}
=\frac{dy}{dx}|_{t=\frac{\pi}{3}}=\frac{\frac{1}{2}-\frac{\sqrt{3} }{2} }{\frac{1}{2}+\frac{\sqrt{3} }{2} }=\sqrt{3}-2
d t d y = ( cos t − sin t ) e t = d t d x = e t ( cos t + sin t ) = d x d y = c o s t + s i n t c o s t − s i n t = d x d y ∣ t = 3 π = 2 1 + 2 3 2 1 − 2 3 = 3 − 2
微分 导数 :f ′ ( x ) = lim Δ x → 0 Δ y Δ x = d y d x 函数的增量 自变量增量 f'(x)=\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}=\frac{dy}{dx} \frac{函数的增量}{自变量增量} f ′ ( x ) = lim Δ x → 0 Δ x Δ y = d x d y 自 变 量 增 量 函 数 的 增 量 微分 :d y = f ′ ( x ) d x dy=f'(x)dx d y = f ′ ( x ) d x 证明
微分的定义 :如果函数的增量Δ y = f ( x 0 + Δ x ) − f ( x 0 ) \Delta y=f(x_0+\Delta x)-f(x_0) Δ y = f ( x 0 + Δ x ) − f ( x 0 ) Δ y = A ⋅ Δ x + o ( Δ x ) \Delta y=A \cdot \Delta x+o(\Delta x) Δ y = A ⋅ Δ x + o ( Δ x ) Δ x \Delta x Δ x y = f ( x ) 在点 x 0 y=f(x)在点x_0 y = f ( x ) 在 点 x 0 可微 的,而A ⋅ Δ x A \cdot \Delta x A ⋅ Δ x d y = A ⋅ Δ x dy=A \cdot \Delta x d y = A ⋅ Δ x d y = A ⋅ Δ x dy=A \cdot \Delta x d y = A ⋅ Δ x d x dx d x 函数可导 ⟵ 等价 ⟶ 函数可微 函数可导\longleftarrow等价 \longrightarrow 函数可微 函 数 可 导 ⟵ 等 价 ⟶ 函 数 可 微 基本微分公式及微分运算法则基本公式 运算法则
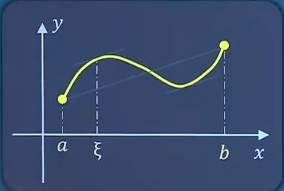
微分中值定理 罗尔中值定理 如果函数f ( x ) f(x) f ( x ) (缺一不可) :
在闭区间[ a , b ] [a,b] [ a , b ]
在开区间( a , b ) (a,b) ( a , b )
f ( a ) = f ( b ) f(a)=f(b) f ( a ) = f ( b ) ( a , b ) (a,b) ( a , b ) ξ \xi ξ f ′ ( ξ ) = 0 f'(\xi)=0 f ′ ( ξ ) = 0 生活实例 不要和零点定理搞混!!! A 、 f ( x ) = { x + 1 , x < 5 1 , x ≥ 5 [ 0 , 5 ] A、f(x)=\left\{\begin{matrix}
x+1,x<5
\\
1, x\ge 5
\end{matrix}\right.
[0,5]
A 、 f ( x ) = { x + 1 , x < 5 1 , x ≥ 5 [ 0 , 5 ] B 、 f ( x ) = ( x − 1 ) 2 3 [ 0 , 2 ] B、f(x)=\sqrt[3]{(x-1)^2} [0,2] B 、 f ( x ) = 3 ( x − 1 ) 2 [ 0 , 2 ] C 、 f ( x ) = x 2 − 3 x + 2 [ 1 , 2 ] C、f(x)= x^2-3x+2 [1,2] C 、 f ( x ) = x 2 − 3 x + 2 [ 1 , 2 ] D 、 f ( x ) = ∣ x − 1 ∣ [ 0 , 2 ] D、f(x)=|x-1| [0,2] D 、 f ( x ) = ∣ x − 1 ∣ [ 0 , 2 ] 3 a 1 x 2 − 2 a 2 x = a 1 − a 2 3a_1x^2-2a_2x=a_1-a_2 3 a 1 x 2 − 2 a 2 x = a 1 − a 2 ( 0 , 1 ) (0,1) ( 0 , 1 ) f ( x ) = 3 a 1 x 2 − 2 a 2 x − a 1 + a 2 f(x)=3a_1x^2-2a_2x-a_1+a_2 f ( x ) = 3 a 1 x 2 − 2 a 2 x − a 1 + a 2 f ( 0 ) = − a 1 + a 2 f(0)=-a_1+a_2 f ( 0 ) = − a 1 + a 2 f ( 1 ) = 2 a 1 − a 2 f(1)=2a_1-a_2 f ( 1 ) = 2 a 1 − a 2 f ′ ( x ) = 3 a 1 x 2 − 2 a 2 x − a 1 + a 2 f'(x)=3a_1x^2-2a_2x-a_1+a_2 f ′ ( x ) = 3 a 1 x 2 − 2 a 2 x − a 1 + a 2 f ( x ) = a 1 x 3 − a 2 x 2 − a 1 x + a 2 x f(x)=a_1x^3-a_2x^2-a_1x+a_2x f ( x ) = a 1 x 3 − a 2 x 2 − a 1 x + a 2 x 答案 标准解题 f ( x ) f(x) f ( x ) x ∈ R x \in R x ∈ R f ( a ) = f ( b ) = 0 f(a)=f(b)=0 f ( a ) = f ( b ) = 0 ξ ∈ ( a , b ) \xi \in (a,b) ξ ∈ ( a , b ) f ′ ( ξ ) + f ( ξ ) = 0 f'(\xi)+f(\xi)=0 f ′ ( ξ ) + f ( ξ ) = 0 f ′ ( ξ ) f'(\xi) f ′ ( ξ ) F ( x ) = f ( x ) ⋅ e x F(x)=f(x) \cdot e^x F ( x ) = f ( x ) ⋅ e x F ( x ) F(x) F ( x ) [ a , b ] [a,b] [ a , b ] ( a , b ) (a,b) ( a , b ) F ( a ) = 0 , F ( b ) = 0 F(a)=0,F(b)=0 F ( a ) = 0 , F ( b ) = 0 F ′ ( x ) = f ′ ( x ) e x + f ( x ) e x F'(x)=f'(x)e^x+f(x)e^x F ′ ( x ) = f ′ ( x ) e x + f ( x ) e x F ( x ) F(x) F ( x ) [ a , b ] [a,b] [ a , b ] ( a , b ) (a,b) ( a , b ) ξ \xi ξ F ′ ( ξ ) = 0 F'(\xi)=0 F ′ ( ξ ) = 0 f ′ ( ξ ) e ξ + f ( ξ ) e ξ = 0 f'(\xi)e^{\xi}+f(\xi)e^{\xi}=0 f ′ ( ξ ) e ξ + f ( ξ ) e ξ = 0 f ′ ( ξ ) + f ( ξ ) = 0 。 f'(\xi)+f(\xi)=0。 f ′ ( ξ ) + f ( ξ ) = 0 。
例题3-2:已知函数f ( x ) f(x) f ( x ) x ∈ R x \in R x ∈ R f ( a ) = f ( b ) = 0 f(a)=f(b)=0 f ( a ) = f ( b ) = 0 ξ ∈ ( a , b ) \xi \in (a,b) ξ ∈ ( a , b ) f ′ ( ξ ) + 2 f ( ξ ) = 0 f'(\xi)+2f(\xi)=0 f ′ ( ξ ) + 2 f ( ξ ) = 0 f ′ ( x ) □ + 2 f ( x ) □ = 0 f'(x)\Box +2f(x)\Box =0 f ′ ( x ) □ + 2 f ( x ) □ = 0 使用 ( u v ) ′ = u ′ v + u v ′ 使用(uv)'=u'v+uv' 使 用 ( u v ) ′ = u ′ v + u v ′ ∴ □ = e 2 x \therefore \Box =e^{2x} ∴ □ = e 2 x F ( x ) = f ( x ) ⋅ e 2 x F(x)=f(x) \cdot e^{2x} F ( x ) = f ( x ) ⋅ e 2 x F ( x ) F(x) F ( x ) [ a , b ] [a,b] [ a , b ] ( a , b ) (a,b) ( a , b ) F ( a ) = 0 , F ( b ) = 0 F(a)=0,F(b)=0 F ( a ) = 0 , F ( b ) = 0 F ′ ( x ) = f ′ ( x ) e 2 x + 2 f ( x ) e 2 x F'(x)=f'(x)e^{2x}+2f(x)e^{2x } F ′ ( x ) = f ′ ( x ) e 2 x + 2 f ( x ) e 2 x F ( x ) F(x) F ( x ) [ a , b ] [a,b] [ a , b ] ( a , b ) (a,b) ( a , b ) ξ \xi ξ F ′ ( ξ ) = 0 F'(\xi)=0 F ′ ( ξ ) = 0 f ′ ( ξ ) + 2 f ( ξ ) = 0 。 f'(\xi)+2f(\xi)=0。 f ′ ( ξ ) + 2 f ( ξ ) = 0 。
例题3-3:已知函数f ( x ) f(x) f ( x ) x ∈ R x \in R x ∈ R f ( a ) = f ( b ) = 0 f(a)=f(b)=0 f ( a ) = f ( b ) = 0 ξ ∈ ( a , b ) \xi \in (a,b) ξ ∈ ( a , b ) f ′ ( ξ ) + 2 ξ f ( ξ ) = 0 f'(\xi)+2\xi f(\xi)=0 f ′ ( ξ ) + 2 ξ f ( ξ ) = 0 f ′ ( x ) □ + 2 x f ( x ) □ = 0 f'(x)\Box +2xf(x)\Box =0 f ′ ( x ) □ + 2 x f ( x ) □ = 0 使用 ( u v ) ′ = u ′ v + u v ′ 使用(uv)'=u'v+uv' 使 用 ( u v ) ′ = u ′ v + u v ′ ∴ □ = e x 2 \therefore \Box =e^{x^2} ∴ □ = e x 2 F ( x ) = f ( x ) ⋅ e x 2 F(x)=f(x) \cdot e^{x^2} F ( x ) = f ( x ) ⋅ e x 2 F ( x ) F(x) F ( x ) [ a , b ] [a,b] [ a , b ] ( a , b ) (a,b) ( a , b ) F ( a ) = 0 , F ( b ) = 0 F(a)=0,F(b)=0 F ( a ) = 0 , F ( b ) = 0 F ′ ( x ) = f ′ ( x ) e x 2 + 2 f ( x ) e x 2 F'(x)=f'(x)e^{x^2}+2f(x)e^{x^2} F ′ ( x ) = f ′ ( x ) e x 2 + 2 f ( x ) e x 2 F ( x ) F(x) F ( x ) [ a , b ] [a,b] [ a , b ] ( a , b ) (a,b) ( a , b ) ξ \xi ξ F ′ ( ξ ) = 0 F'(\xi)=0 F ′ ( ξ ) = 0 f ′ ( ξ ) + 2 ξ f ( ξ ) = 0 。 f'(\xi)+2\xi f(\xi)=0。 f ′ ( ξ ) + 2 ξ f ( ξ ) = 0 。
例题3-4:已知函数f ( x ) f(x) f ( x ) x ∈ R x \in R x ∈ R f ( a ) = f ( b ) = 0 f(a)=f(b)=0 f ( a ) = f ( b ) = 0 ξ ∈ ( a , b ) \xi \in (a,b) ξ ∈ ( a , b ) ξ n f ′ ( ξ ) + f ( ξ ) = 0 , n \frac{\xi}{n}f'(\xi)+f(\xi)=0,n n ξ f ′ ( ξ ) + f ( ξ ) = 0 , n f ′ ( x ) x n □ + f ( x ) □ = 0 f'(x)\frac{x}{n} \Box +f(x)\Box =0 f ′ ( x ) n x □ + f ( x ) □ = 0 使用 ( u v ) ′ = u ′ v + u v ′ 使用(uv)'=u'v+uv' 使 用 ( u v ) ′ = u ′ v + u v ′ ∴ □ = x n \therefore \Box =x^n ∴ □ = x n F ( x ) = f ( x ) ⋅ x n F(x)=f(x) \cdot x^n F ( x ) = f ( x ) ⋅ x n F ( x ) F(x) F ( x ) [ a , b ] [a,b] [ a , b ] ( a , b ) (a,b) ( a , b ) F ( a ) = 0 , F ( b ) = 0 F(a)=0,F(b)=0 F ( a ) = 0 , F ( b ) = 0 F ′ ( x ) = f ′ ( x ) ⋅ x n + f ( x ) ⋅ n x ⋅ x n F'(x)=f'(x) \cdot x^n+f(x) \cdot \frac{n}{x}\cdot x^n F ′ ( x ) = f ′ ( x ) ⋅ x n + f ( x ) ⋅ x n ⋅ x n F ( x ) F(x) F ( x ) [ a , b ] [a,b] [ a , b ] ( a , b ) (a,b) ( a , b ) ξ \xi ξ F ′ ( ξ ) = 0 F'(\xi)=0 F ′ ( ξ ) = 0 f ′ ( ξ ) ⋅ ξ n + f ( ξ ) ⋅ n ξ ⋅ ξ n = 0 。 f'(\xi) \cdot \xi ^n+f(\xi) \cdot \frac{n}{\xi} \cdot \xi ^n=0。 f ′ ( ξ ) ⋅ ξ n + f ( ξ ) ⋅ ξ n ⋅ ξ n = 0 。 ξ n f ′ ( ξ ) + f ( ξ ) = 0 。 \frac{\xi }{n} f'(\xi)+f(\xi)=0。 n ξ f ′ ( ξ ) + f ( ξ ) = 0 。 f ( x ) f(x) f ( x ) x ∈ R x \in R x ∈ R f ( a ) = f ( b ) = 0 f(a)=f(b)=0 f ( a ) = f ( b ) = 0 ξ ∈ ( a , b ) \xi \in (a,b) ξ ∈ ( a , b ) f ′ ( ξ ) − f ( ξ ) = 0 f'(\xi)-f(\xi)=0 f ′ ( ξ ) − f ( ξ ) = 0 f ′ ( x ) □ − f ( x ) □ = 0 f'(x) \Box -f(x)\Box =0 f ′ ( x ) □ − f ( x ) □ = 0 使用 ( u v ) ′ = u ′ v − u v ′ v 2 使用(\frac{u}{v})'=\frac{u'v-uv'}{v^2} 使 用 ( v u ) ′ = v 2 u ′ v − u v ′ ∴ □ = e x \therefore \Box =e^x ∴ □ = e x F ( x ) = f ( x ) e x F(x)=\frac{f(x)}{e^x} F ( x ) = e x f ( x ) F ( x ) F(x) F ( x ) [ a , b ] [a,b] [ a , b ] ( a , b ) (a,b) ( a , b ) F ( a ) = 0 , F ( b ) = 0 F(a)=0,F(b)=0 F ( a ) = 0 , F ( b ) = 0 F ′ ( x ) = f ′ ( x ) ⋅ e x − f ( x ) ⋅ e x ( e x ) 2 F'(x)=\frac{f'(x)\cdot e^x-f(x)\cdot e^x}{(e^x)^2} F ′ ( x ) = ( e x ) 2 f ′ ( x ) ⋅ e x − f ( x ) ⋅ e x F ( x ) F(x) F ( x ) [ a , b ] [a,b] [ a , b ] ( a , b ) (a,b) ( a , b ) ξ \xi ξ F ′ ( ξ ) = 0 F'(\xi)=0 F ′ ( ξ ) = 0 f ′ ( ξ ) ⋅ e ξ − f ( ξ ) ⋅ e ξ ( e ξ ) 2 = 0 \frac{f'(\xi)\cdot e^\xi-f(\xi) \cdot e^\xi}{(e^\xi)^2}=0 ( e ξ ) 2 f ′ ( ξ ) ⋅ e ξ − f ( ξ ) ⋅ e ξ = 0 f ′ ( ξ ) − f ( ξ ) = 0 f'(\xi)-f(\xi)=0 f ′ ( ξ ) − f ( ξ ) = 0
例题:若f ( x ) f(x) f ( x ) [ 1 , e ] [1,e] [ 1 , e ] ( 1 , e ) (1,e) ( 1 , e ) f ( 1 ) = 0 , f ( e ) = 1 f(1)=0,f(e)=1 f ( 1 ) = 0 , f ( e ) = 1 ξ ∈ ( 1 , e ) \xi \in (1,e) ξ ∈ ( 1 , e ) ξ ⋅ f ′ ( ξ ) = 1 \xi \cdot f'(\xi )=1 ξ ⋅ f ′ ( ξ ) = 1 F ( x ) = f ( x ) ⋅ ln x F(x)=f(x) \cdot \ln x F ( x ) = f ( x ) ⋅ ln x F ′ ( x ) = f ′ ( x ) − 1 2 F'(x)=f'(x)-\frac{1}{2} F ′ ( x ) = f ′ ( x ) − 2 1 F ( 1 ) = 0 , F ( e ) = 1 F(1)=0,F(e)=1 F ( 1 ) = 0 , F ( e ) = 1 F ′ ( 1 ) = f ′ ( 1 ) − ln 1 = 0 F'(1)=f'(1)-\ln 1=0 F ′ ( 1 ) = f ′ ( 1 ) − ln 1 = 0 F ′ ( e ) = f ( e ) − ln e = 0 F'(e)=f(e)-\ln e=0 F ′ ( e ) = f ( e ) − ln e = 0 f ′ ( 1 ) = f ′ ( e ) = 0 f'(1)=f'(e)=0 f ′ ( 1 ) = f ′ ( e ) = 0 ξ ∈ ( 1 , e ) \xi \in (1,e) ξ ∈ ( 1 , e ) F ′ ( ξ ) = 0 F'(\xi)=0 F ′ ( ξ ) = 0 f ′ ( ξ ) − 1 ξ = 0 f'(\xi)-\frac{1}{\xi}=0 f ′ ( ξ ) − ξ 1 = 0 f ′ ( ξ ) = 1 ξ f'(\xi)=\frac{1}{\xi} f ′ ( ξ ) = ξ 1 ξ f ′ ( ξ ) = 1 \xi f'(\xi)=1 ξ f ′ ( ξ ) = 1
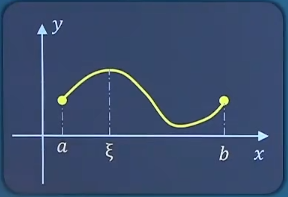
拉格朗日中值定理 如果函数y = f ( x ) y=f(x) y = f ( x ) (缺一不可) :
在闭区间[ a , b ] [a,b] [ a , b ]
在开区间( a , b ) (a,b) ( a , b ) ( a , b ) (a,b) ( a , b ) ξ \xi ξ f ′ ( ξ ) = f ( b ) − f ( a ) b − a f'(\xi)=\frac{f(b)-f(a)}{b-a} f ′ ( ξ ) = b − a f ( b ) − f ( a ) f ( x ) = e x − 3 x 1 3 f(x)=e^x-3x^{\frac{1}{3} } f ( x ) = e x − 3 x 3 1 [ − 1 , 0 ] [-1,0] [ − 1 , 0 ] [ 0 , 1 ] [0,1] [ 0 , 1 ] [ − 1 , 1 ] [-1,1] [ − 1 , 1 ] [ 1 , e ] [1,e] [ 1 , e ] f ( x ) f(x) f ( x ) f ′ ( x ) , 看 f ′ ( x ) f'(x),看f'(x) f ′ ( x ) , 看 f ′ ( x ) f ′ ( x ) = e x − 1 x 2 3 ( x ≠ 0 ) f'(x)=e^x-\frac{1}{\sqrt[3]{x^2} }(x \ne 0) f ′ ( x ) = e x − 3 x 2 1 ( x = 0 )
例题2:函数f ( x ) = 1 2 x 2 − x f(x)=\frac{1}{2}x^2-x f ( x ) = 2 1 x 2 − x [ 1 , 2 ] [1,2] [ 1 , 2 ] ξ = ( 3 2 ) \xi=( \frac{3}{2} ) ξ = ( 2 3 ) f ′ ( x ) = x − 1 f'(x)=x-1 f ′ ( x ) = x − 1 f ( 1 ) = 1 2 ⋅ 1 2 − 1 = − 1 2 f(1)=\frac{1}{2} \cdot 1^2-1=-\frac{1}{2} f ( 1 ) = 2 1 ⋅ 1 2 − 1 = − 2 1 f ( 2 ) = 1 2 ⋅ 2 2 − 2 = 0 f(2)=\frac{1}{2} \cdot 2^2-2=0 f ( 2 ) = 2 1 ⋅ 2 2 − 2 = 0 ∴ f ( 2 ) − f ( 1 ) 2 − 1 = 1 2 \therefore \frac{f(2)-f(1)}{2-1}=\frac{1}{2} ∴ 2 − 1 f ( 2 ) − f ( 1 ) = 2 1 ∴ ξ = 1 + 1 2 = 3 2 \therefore \xi=1+\frac{1}{2}=\frac{3}{2} ∴ ξ = 1 + 2 1 = 2 3
例题3-1:设0 < b < c 0<b<c 0 < b < c b − a 1 + b 2 < arctan b − arctan a < b − a 1 + a 2 \frac{b-a}{1+b^2}<\arctan b-\arctan a<\frac{b-a}{1+a^2} 1 + b 2 b − a < arctan b − arctan a < 1 + a 2 b − a f ( x ) = arctan x f(x)=\arctan x f ( x ) = arctan x f ( x ) f(x) f ( x ) [ a , b ] [a,b] [ a , b ] ( a , b ) (a,b) ( a , b ) f ( x ) f(x) f ( x ) [ a , b ] [a,b] [ a , b ] ( a , b ) (a,b) ( a , b ) ξ \xi ξ f ′ ( ξ ) = arctan b − arctan a b − a f'(\xi)=\frac{\arctan b-\arctan a}{b-a} f ′ ( ξ ) = b − a a r c t a n b − a r c t a n a f ′ ( ξ ) = 1 1 + ξ 2 , arctan b − arctan a = b − a 1 + ξ 2 f'(\xi)=\frac{1}{1+\xi^2},\arctan b-\arctan a=\frac{b-a}{1+\xi^2} f ′ ( ξ ) = 1 + ξ 2 1 , arctan b − arctan a = 1 + ξ 2 b − a a < ξ < b a<\xi<b a < ξ < b b − a 1 + b 2 < b − a 1 + ξ 2 < b − a 1 + a 2 \frac{b-a}{1+b^2}<\frac{b-a}{1+\xi^2}<\frac{b-a}{1+a^2} 1 + b 2 b − a < 1 + ξ 2 b − a < 1 + a 2 b − a b − a 1 + b 2 < arctan b − arctan a < b − a 1 + a 2 \frac{b-a}{1+b^2}<\arctan b-\arctan a<\frac{b-a}{1+a^2} 1 + b 2 b − a < arctan b − arctan a < 1 + a 2 b − a
例题3-2:设x > 0 x>0 x > 0 x 1 + x < l n ( 1 + x ) < x \frac{x}{1+x}<ln(1+x)<x 1 + x x < l n ( 1 + x ) < x f ( x ) = l n ( x ) f(x)=ln(x) f ( x ) = l n ( x ) f ( x ) f(x) f ( x ) [ 1 , 1 + x ] [1,1+x] [ 1 , 1 + x ] ( 1 , 1 + x ) (1,1+x) ( 1 , 1 + x ) f ( x ) f(x) f ( x ) [ 1 , 1 + x ] [1,1+x] [ 1 , 1 + x ] ( 1 , 1 + x ) (1,1+x) ( 1 , 1 + x ) ξ \xi ξ f ′ ( ξ ) = l n ( 1 + x ) − l n 1 1 + x − 1 = l n ( 1 + x ) x f'(\xi)=\frac{ln(1+x)-ln1}{1+x-1}=\frac{ln(1+x)}{x} f ′ ( ξ ) = 1 + x − 1 l n ( 1 + x ) − l n 1 = x l n ( 1 + x ) f ′ ( ξ ) = 1 ξ , l n ( 1 + x ) − l n 1 = x ⋅ 1 ξ = x ξ f'(\xi)=\frac{1}{\xi},ln(1+x)-ln1=x \cdot \frac{1}{\xi}=\frac{x}{\xi} f ′ ( ξ ) = ξ 1 , l n ( 1 + x ) − l n 1 = x ⋅ ξ 1 = ξ x 1 < ξ < 1 + x 1<\xi<1+x 1 < ξ < 1 + x x 1 + x < x ξ < x \frac{x}{1+x}<\frac{x}{\xi}<x 1 + x x < ξ x < x x 1 + x < l n ( 1 + x ) < x \frac{x}{1+x}<ln(1+x)<x 1 + x x < l n ( 1 + x ) < x
例题3-3:设x ∈ ( 0 , π 2 ) x \in (0,\frac{\pi}{2}) x ∈ ( 0 , 2 π ) x < tan x < x cos 2 x x<\tan x<\frac{x}{\cos ^2x} x < tan x < c o s 2 x x f ( x ) = tan x f(x)=\tan x f ( x ) = tan x f ( x ) f(x) f ( x ) [ 0 , x ] [0,x] [ 0 , x ] ( 0 , x ) (0,x) ( 0 , x ) f ( x ) f(x) f ( x ) [ 0 , x ] [0,x] [ 0 , x ] ( 0 , x ) (0,x) ( 0 , x ) ξ \xi ξ f ′ ( ξ ) = tan x − tan 0 x − 0 = tan x x f'(\xi)=\frac{\tan x-\tan 0}{x-0}=\frac{\tan x}{x} f ′ ( ξ ) = x − 0 t a n x − t a n 0 = x t a n x f ′ ( ξ ) = 1 cos 2 ξ , tan x − tan 0 = x ⋅ 1 cos 2 ξ = x cos 2 ξ f'(\xi)=\frac{1}{\cos ^2\xi},\tan x-\tan 0=x \cdot \frac{1}{\cos ^2\xi}=\frac{x}{\cos ^2\xi} f ′ ( ξ ) = c o s 2 ξ 1 , tan x − tan 0 = x ⋅ c o s 2 ξ 1 = c o s 2 ξ x 0 < ξ < x 0<\xi<x 0 < ξ < x x < x cos 2 ξ < x cos 2 x x<\frac{x}{\cos ^2\xi}<\frac{x}{\cos ^2x} x < c o s 2 ξ x < c o s 2 x x x < tan x < x cos 2 x x<\tan x<\frac{x}{\cos ^2x} x < tan x < c o s 2 x x
例题3总结:
柯西中值定理 洛必达法则 lim x → x 0 / x → ∞ f ( x ) g ( x ) = lim x → x 0 / x → ∞ f ′ ( x ) g ′ ( x ) \lim_{x \to x_0/x \to \infty }\frac{f(x)}{g(x)}= \lim_{x \to x_0/x \to \infty }\frac{f'(x) } {g'(x)} lim x → x 0 / x → ∞ g ( x ) f ( x ) = lim x → x 0 / x → ∞ g ′ ( x ) f ′ ( x ) 两函数之商求极限等于两函数导数之商的极限。
f ( x ) , g ( x ) f(x),g(x) f ( x ) , g ( x ) ∞ \infty ∞ 0 0 \frac{0}{0} 0 0 ∞ ∞ \frac{ \infty }{ \infty } ∞ ∞ lim x → x 0 / x → ∞ f ′ ( x ) g ′ ( x ) \lim_{x \to x_0/x \to \infty }\frac{f'(x)}{g'(x)} lim x → x 0 / x → ∞ g ′ ( x ) f ′ ( x ) ∞ \infty ∞ 同一道题中洛必达可以和等价无穷小可以交替使用,但是同一步骤中绝对不能混用 非0非无穷因子可先带入,可简化计算。(条件:整体的极限式子可看作是非0非无穷因子和,另外一个式子的乘积的形式,局部加减的非0非无穷式子不能先行带入!)
例题1:求lim x → + ∞ x 100 e x \lim_{x \to +\infty}\frac{x^{100} }{e^x} lim x → + ∞ e x x 1 0 0 lim x → + ∞ 100 x 99 e x = lim x → + ∞ 9900 x 98 e x = lim x → + ∞ 980100 x 97 e x = lim x → + ∞ 97029900 x 96 e x … … = lim x → + ∞ 100 ! x 0 e x = 0 \lim_{x \to +\infty}\frac{100x^{99} }{e^x}
=\lim_{x \to +\infty}\frac{9900x^{98} }{e^x}
=\lim_{x \to +\infty}\frac{980100x^{97} }{e^x}
=\lim_{x \to +\infty}\frac{97029900x^{96} }{e^x}
……
=\lim_{x \to +\infty}\frac{100!x^0}{e^x}
=0 lim x → + ∞ e x 1 0 0 x 9 9 = lim x → + ∞ e x 9 9 0 0 x 9 8 = lim x → + ∞ e x 9 8 0 1 0 0 x 9 7 = lim x → + ∞ e x 9 7 0 2 9 9 0 0 x 9 6 … … = lim x → + ∞ e x 1 0 0 ! x 0 = 0 lim x → 0 s − sin x x 2 sin x \lim_{x \to 0}\frac{s-\sin x}{x^2 \sin x} lim x → 0 x 2 s i n x s − s i n x = lim x → 0 x − sin x x 3 = lim x → 0 1 − cos x 3 x 2 = lim x → 0 sin x 6 x = lim x → 0 x 6 x = 1 6 =\lim_{x \to 0}\frac{x-\sin x}{x3}
=\lim_{x \to 0}\frac{1-\cos x}{3x^2}
=\lim_{x \to 0}\frac{\sin x}{6x}
=\lim_{x \to 0}\frac{x}{6x}
=\frac{1}{6} = lim x → 0 x 3 x − s i n x = lim x → 0 3 x 2 1 − c o s x = lim x → 0 6 x s i n x = lim x → 0 6 x x = 6 1 x → 0 时, ( x − sin x ) 1 6 x 3 {\color{Red} x \to 0 时,(x-\sin x)~\frac{1}{6}x^3} x → 0 时 , ( x − s i n x ) 6 1 x 3 lim x → 0 tan x − x x − sin x \lim_{x \to 0}\frac{\tan x-x}{x-\sin x} lim x → 0 x − s i n x t a n x − x = lim x → 0 1 cos 2 x − 1 1 − cos x = lim x → 0 1 + cos x cos 2 x = lim x → 0 1 + 1 1 = 2 =\lim_{x \to 0}\frac{\frac{1}{\cos ^2x}-1}{1-\cos x}
=\lim_{x \to 0}\frac{1+\cos x}{\cos ^2x}
=\lim_{x \to 0}\frac{1+1}{1}
=2 = lim x → 0 1 − c o s x c o s 2 x 1 − 1 = lim x → 0 c o s 2 x 1 + c o s x = lim x → 0 1 1 + 1 = 2 x → 0 时, ( tan x − x ) 1 3 x 3 {\color{Red} x \to 0 时,(\tan x-x)~\frac{1}{3}x^3} x → 0 时 , ( t a n x − x ) 3 1 x 3 lim x → π 2 e x ⋅ cos x π 2 − x \lim_{x \to \frac{\pi}{2} }\frac{e^x \cdot \cos x}{\frac{\pi}{2}-x} lim x → 2 π 2 π − x e x ⋅ c o s x = e π 2 lim x → π 2 cos x π 2 − x = e π 2 lim x → π 2 − sin x − 1 = e π 2 lim x → π 2 − 1 − 1 = e π 2 =e^{\frac{\pi}{2} } \lim_{x \to \frac{\pi}{2} }\frac{\cos x}{\frac{\pi}{2}-x}
=e^{\frac{\pi}{2} } \lim_{x \to \frac{\pi}{2} }\frac{-\sin x}{-1}
=e^{\frac{\pi}{2} } \lim_{x \to \frac{\pi}{2} }\frac{-1}{-1}
=e^{\frac{\pi}{2} } = e 2 π lim x → 2 π 2 π − x c o s x = e 2 π lim x → 2 π − 1 − s i n x = e 2 π lim x → 2 π − 1 − 1 = e 2 π lim x → ∞ sin x − x cos x x 3 cos x \lim_{x \to \infty}\frac{\sin x-x \cos x}{x^3 \cos x} lim x → ∞ x 3 c o s x s i n x − x c o s x = 1 cos 0 ⋅ lim x → ∞ sin x − x ⋅ cos x x 3 = 1 ⋅ lim x → ∞ cos x − ( cos x − x ⋅ sin x ) 3 x 2 = lim x → ∞ x ⋅ sin x 3 x 2 = lim x → ∞ sin x 3 x = 1 3 =\frac{1}{\cos 0} \cdot \lim_{x \to \infty}\frac{\sin x- x \cdot \cos x}{x^3}
=1 \cdot \lim_{x \to \infty}\frac{\cos x- (\cos x -x \cdot \sin x) }{3x^2}
=\lim_{x \to \infty}\frac{x \cdot \sin x}{3x^2}
=\lim_{x \to \infty}\frac{\sin x}{3x}
=\frac{1}{3} = c o s 0 1 ⋅ lim x → ∞ x 3 s i n x − x ⋅ c o s x = 1 ⋅ lim x → ∞ 3 x 2 c o s x − ( c o s x − x ⋅ s i n x ) = lim x → ∞ 3 x 2 x ⋅ s i n x = lim x → ∞ 3 x s i n x = 3 1 lim x → ∞ sin x + x x \lim_{x \to \infty}\frac{\sin x+x}{x} lim x → ∞ x s i n x + x = lim x → ∞ sin x x + 1 = 0 + 1 = 1 =\lim_{x \to \infty}\frac{\sin x}{x}+1
=0+1
=1 = lim x → ∞ x s i n x + 1 = 0 + 1 = 1 lim x → ∞ e x − e − x e + e − x \lim_{x \to \infty}\frac{e^x-e{-x} }{e^+e{-x} } lim x → ∞ e + e − x e x − e − x 上下同除以 e x = lim x → ∞ 1 + 1 ( e x ) 2 1 − 1 ( e x ) 2 = 1 + 0 1 − 0 = 1 上下同除以e^x
=\lim_{x \to \infty}\frac{1+\frac{1}{(e^x)^2} }{1-\frac{1}{(e^x)^2} }
=\frac{1+0}{1-0}
=1 上 下 同 除 以 e x = lim x → ∞ 1 − ( e x ) 2 1 1 + ( e x ) 2 1 = 1 − 0 1 + 0 = 1
总结
0 0 \frac{0}{0} 0 0 或
∞ ∞ \frac{\infty}{\infty} ∞ ∞ 型
l i m f ( x ) g ( x ) = l i m f ′ ( x ) g ′ ( x ) = l i m f ′ ′ ( x ) g ′ ′ ( x ) = … … = A lim{\frac{f(x)}{g(x)}}=lim{\frac{f'(x)}{g'(x)}}=lim{\frac{f''(x)}{g''(x)}}=……=A l i m g ( x ) f ( x ) = l i m g ′ ( x ) f ′ ( x ) = l i m g ′ ′ ( x ) f ′ ′ ( x ) = … … = A 注意:
分子分母各自同时求导;
洛必达法则一般配合等价使用;
导数在研究函数中的应用 切线方程与法线方程 函数在某一点处的导数的几何意义即在该点处切线的斜率 。法线和切线垂直 ,如果两条直线垂直,那么斜率之积=-1 。( x 0 , y 0 ) (x_0,y_0) ( x 0 , y 0 ) k k k y − y 0 = k ( x − x 0 ) y-y_0=k(x-x_0) y − y 0 = k ( x − x 0 ) k 切 = f ′ ( x 0 ) , K 法 = − 1 f ′ ( x 0 ) k_切=f'(x_0), K_法=-\frac{1}{f'(x_0) } k 切 = f ′ ( x 0 ) , K 法 = − f ′ ( x 0 ) 1 y 0 y_0 y 0 f ′ ( x 0 ) f'(x_0) f ′ ( x 0 ) f ′ ( x ) f'(x) f ′ ( x ) x 0 x_0 x 0 y − y 0 = f ′ ( x 0 ) ( x − x 0 ) y-y_0=f'(x_0)(x-x_0) y − y 0 = f ′ ( x 0 ) ( x − x 0 ) y − y 0 = − 1 f ′ ( x 0 ) ( x − x 0 ) y-y_0=-\frac{1}{f'(x_0) } (x-x_0) y − y 0 = − f ′ ( x 0 ) 1 ( x − x 0 ) f ( x ) = x 2 − 3 x + 1 f(x)=x^2-3x+1 f ( x ) = x 2 − 3 x + 1 ( 1 , − 1 ) (1,-1) ( 1 , − 1 ) f ′ ( x ) = 2 x − 3 f'(x)=2x-3 f ′ ( x ) = 2 x − 3 x = 1 x=1 x = 1 f ′ ( x ) = 2 ⋅ 1 − 3 = − 1 f'(x)=2 \cdot 1-3=-1 f ′ ( x ) = 2 ⋅ 1 − 3 = − 1 y − ( − 1 ) = − 1 ( x − 1 ) y-(-1)=-1(x-1) y − ( − 1 ) = − 1 ( x − 1 ) y = − x y=-x y = − x y − ( − 1 ) = − 1 − 1 ( x − 1 ) y-(-1)=-\frac{1}{-1}(x-1) y − ( − 1 ) = − − 1 1 ( x − 1 ) y = x − 2 y=x-2 y = x − 2 y = 2 e x y=2e^x y = 2 e x x = 0 x=0 x = 0 如果题目只告诉了x,那这个x带入原方程求y y = 2 e 0 = 2 y=2e^0=2 y = 2 e 0 = 2 f ′ ( x ) = 2 e x f'(x)=2e^x f ′ ( x ) = 2 e x x = 0 x=0 x = 0 f ′ ( x 0 ) = 2 e 0 = 2 f'(x_0)=2e^0=2 f ′ ( x 0 ) = 2 e 0 = 2 y − 2 = 2 ( x − 0 ) y-2=2(x-0) y − 2 = 2 ( x − 0 ) y = 2 x + 2 y=2x+2 y = 2 x + 2 y − 2 = − 1 2 ( x − 0 ) y-2=-\frac{1}{2}(x-0) y − 2 = − 2 1 ( x − 0 ) y = − 1 2 x + 2 y=-\frac{1}{2}x+2 y = − 2 1 x + 2 f ( x ) = 1 − x 3 f(x)=1-x^3 f ( x ) = 1 − x 3 g ( x ) = l n x g(x)=lnx g ( x ) = l n x y = a y=a y = a a = 1 3 a=\frac{1}{3} a = 3 1 K f ⋅ K g = − 1 K_f \cdot K_g=-1 K f ⋅ K g = − 1 f ′ ( a ) = − 3 a 2 f'(a)=-3a^2 f ′ ( a ) = − 3 a 2 g ′ ( a ) = 1 a g'(a)=\frac{1}{a} g ′ ( a ) = a 1 f ′ ( a ) ⋅ g ′ ( a ) = − 3 a 2 ⋅ 1 a = − 3 a = − 1 f'(a) \cdot g'(a)=-3a^2 \cdot \frac{1}{a}=-3a=-1 f ′ ( a ) ⋅ g ′ ( a ) = − 3 a 2 ⋅ a 1 = − 3 a = − 1 a = 1 3 a=\frac{1}{3} a = 3 1
函数的单调性
导数
函数单调性
f’(x)>0
单调增加
f’(x)<0
单调减少
当f ′ ( x ) = 0 f'(x)=0 f ′ ( x ) = 0 f ′ ( x ) f'(x) f ′ ( x ) f ′ ( x ) = 0 f'(x)=0 f ′ ( x ) = 0 f ′ ( x ) f'(x) f ′ ( x ) f ( x ) f(x) f ( x ) f ′ ( x ) f'(x) f ′ ( x ) f ′ ( x ) f'(x) f ′ ( x ) f ( x ) = x + 1 x f(x)=x+\frac{1}{x} f ( x ) = x + x 1 ( − ∞ , 0 ) ∪ ( 0 , + ∞ ) (-\infty,0)\cup (0,+\infty) ( − ∞ , 0 ) ∪ ( 0 , + ∞ ) x = 0 x=0 x = 0 f ′ ( x ) = 1 − 1 x 2 f'(x)=1-\frac{1}{x^2} f ′ ( x ) = 1 − x 2 1 f ′ ( x ) = 0 f'(x)=0 f ′ ( x ) = 0 x = 1 x=1 x = 1 x = − 1 x=-1 x = − 1 x = 0 x=0 x = 0
(-∞,-1)
-1
(-1,0)
0
(0,1)
1
(1,+∞)
f’(x)
+
0
-
×
-
0
+
f(x)
单增
单减
单减
单增
由上表可知,单增( − ∞ , − 1 ) (-\infty,-1) ( − ∞ , − 1 ) ( 1 , + ∞ ) (1,+\infty) ( 1 , + ∞ ) ( − 1 , 0 ) (-1,0) ( − 1 , 0 ) ( 0 , 1 ) (0,1) ( 0 , 1 ) F ( x ) = 左边 − 右边 F(x)=左边-右边 F ( x ) = 左 边 − 右 边 F ′ ( x ) F'(x) F ′ ( x ) F ′ ( x ) F'(x) F ′ ( x ) F ( x ) F(x) F ( x ) F ( x ) > 0 F(x)>0 F ( x ) > 0 F ( x ) < 0 F(x)<0 F ( x ) < 0 x > 0 x>0 x > 0 ln ( 1 + x ) < x \ln (1+x)<x ln ( 1 + x ) < x F ( x ) = ln ( 1 + x ) − x F(x)=\ln (1+x)-x F ( x ) = ln ( 1 + x ) − x F ′ ( x ) = 1 1 + x − 1 = 1 − ( 1 + x ) 1 + x F'(x)=\frac{1}{1+x}-1=\frac{1-(1+x)}{1+x} F ′ ( x ) = 1 + x 1 − 1 = 1 + x 1 − ( 1 + x ) F ′ ( x ) > 0 F'(x)>0 F ′ ( x ) > 0 F ( x ) < 0 F(x)<0 F ( x ) < 0 ∴ F ( 0 ) = 0 \therefore F(0)=0 ∴ F ( 0 ) = 0 [ 0 , + ∞ ) [0,+\infty) [ 0 , + ∞ ) F ( x ) > 0 F(x)>0 F ( x ) > 0 F ( x ) < F ( 0 ) = ln ( 1 + 0 ) − 0 = 0 F(x)<F(0)=\ln (1+0)-0=0 F ( x ) < F ( 0 ) = ln ( 1 + 0 ) − 0 = 0 ln ( 1 + x ) − x < 0 \ln (1+x)-x<0 ln ( 1 + x ) − x < 0 ln ( 1 + x ) < x \ln (1+x)<x ln ( 1 + x ) < x x > sin x x>\sin x x > sin x x ∈ ( 0 , π ) x\in (0,\pi) x ∈ ( 0 , π ) F ( x ) = x − sin x F(x)=x-\sin x F ( x ) = x − sin x F ′ ( x ) = 1 − cos x F'(x)=1-\cos x F ′ ( x ) = 1 − cos x x ∈ ( 0 , π ) , F ′ ( x ) > 0 x \in (0, \pi),F'(x)>0 x ∈ ( 0 , π ) , F ′ ( x ) > 0 ∴ F ( x ) \therefore F(x) ∴ F ( x ) [ 0 , π ) [0,\pi) [ 0 , π ) x ∈ ( 0 , π ) x \in (0,\pi) x ∈ ( 0 , π ) F ( x ) > F ( 0 ) = 0 − sin 0 = 0 F(x)>F(0)=0-\sin 0=0 F ( x ) > F ( 0 ) = 0 − sin 0 = 0 x − sin x > 0 x-\sin x>0 x − sin x > 0 x > sin x x>\sin x x > sin x
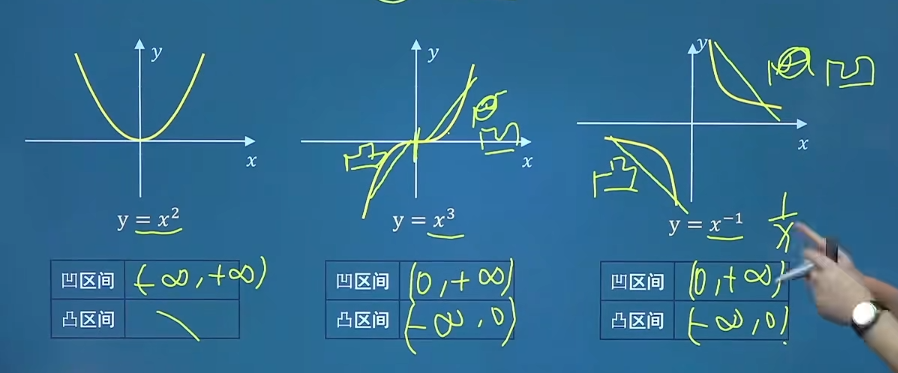
函数曲线的凹凸性 图像的凹凸性
连续曲线凹与凸的分界点称为曲线的拐点。f ( x ) ′ f(x)' f ( x ) ′ f ( x ) ′ ′ < 0 f(x)''<0 f ( x ) ′ ′ < 0 f ( x ) ′ f(x)' f ( x ) ′ f ( x ) ′ ′ > 0 f(x)''>0 f ( x ) ′ ′ > 0
二阶导数
凹凸性
f ′ ′ ( x ) > 0 f''(x)>0 f ′ ′ ( x ) > 0 凹
f ′ ′ ( x ) < 0 f''(x)<0 f ′ ′ ( x ) < 0 凸
不要和函数单调性搞混淆!!!
求函数凹凸区间和拐点的步骤(对比单调区间四步骤):f ( x ) f(x) f ( x ) f ′ ( x ) f'(x) f ′ ( x ) f ′ ′ ( x ) f''(x) f ′ ′ ( x ) f ′ ′ ( x ) = 0 f''(x)=0 f ′ ′ ( x ) = 0 f ′ ′ ( x ) f''(x) f ′ ′ ( x ) f ′ ′ ( x ) f''(x) f ′ ′ ( x ) 拐点是曲线上的点,拐点两侧f ( x ) ′ ′ f(x)'' f ( x ) ′ ′
例题1:求函数f ( x ) = x 4 − 2 x 3 + 3 f(x)=x^4-2x^3+3 f ( x ) = x 4 − 2 x 3 + 3 ( − ∞ , + ∞ ) (-\infty,+\infty) ( − ∞ , + ∞ ) f ′ ( x ) = 4 x 3 − 6 x 2 f'(x)=4x^3-6x^2 f ′ ( x ) = 4 x 3 − 6 x 2 f ′ ′ ( x ) = 12 x 2 − 12 x f''(x)=12x^2-12x f ′ ′ ( x ) = 1 2 x 2 − 1 2 x f ′ ′ ( x ) = 0 f''(x)=0 f ′ ′ ( x ) = 0 x = 0 x=0 x = 0 x = 1 x=1 x = 1
(-∞,0)
0
(0,1)
1
(1,+∞)
f’‘(x)
+
0
-
0
+
曲线
凹
凸
凹
由上表可知,凹区间为( − ∞ , 0 ) (-\infty,0) ( − ∞ , 0 ) ( 0 , 1 ) (0,1) ( 0 , 1 ) ( 0 , 1 ) (0,1) ( 0 , 1 ) ( 1 , + ∞ ) (1,+\infty) ( 1 , + ∞ ) x = 0 x=0 x = 0 f ( 0 ) = 3 f(0)=3 f ( 0 ) = 3 x = 1 x=1 x = 1 f ( 1 ) = 2 f(1)=2 f ( 1 ) = 2 ( 0 , 3 ) (0,3) ( 0 , 3 ) ( 1 , 2 ) (1,2) ( 1 , 2 ) f ( x ) = x 3 f(x)=\sqrt[3]{x} f ( x ) = 3 x [ − ∞ , + ∞ ) [-\infty,+\infty) [ − ∞ , + ∞ ) f ′ ( x ) = 1 3 x − 2 3 f'(x)=\frac{1}{3}x^{-\frac{2}{3} } f ′ ( x ) = 3 1 x − 3 2 f ′ ′ ( x ) = − 2 9 x − 5 3 f''(x)=-\frac{2}{9}x^{-\frac{5}{3} } f ′ ′ ( x ) = − 9 2 x − 3 5 f ′ ′ ( x ) = 0 f''(x)=0 f ′ ′ ( x ) = 0 x = 0 x=0 x = 0 f ′ ′ ( x ) = 0 f''(x)=0 f ′ ′ ( x ) = 0 f ′ ′ ( x ) 不存在的点为 x = 0 f''(x)不存在的点为x=0 f ′ ′ ( x ) 不 存 在 的 点 为 x = 0
(-∞,0)
0
(0,+∞)
f’‘(x)
+
不存在
-
曲线
凹
凸
由上表可知,凹区间为( − ∞ , 0 ) (-\infty,0) ( − ∞ , 0 ) ( 0 , + ∞ ) (0,+\infty) ( 0 , + ∞ ) x = 0 x=0 x = 0 f ( 0 ) = 0 f(0)=0 f ( 0 ) = 0 ( 0 , 0 ) (0,0) ( 0 , 0 )
例题3:函数f ( x ) = x 4 f(x)=x^4 f ( x ) = x 4 f ′ ( x ) = 4 x 3 f'(x)=4x^3 f ′ ( x ) = 4 x 3 f ′ ′ ( x ) = 12 x 2 f''(x)=12x^2 f ′ ′ ( x ) = 1 2 x 2 f ′ ′ ( x ) = 0 f''(x)=0 f ′ ′ ( x ) = 0 x = 0 x=0 x = 0
(-∞,0)
0
(0,+∞)
f’‘(x)
+
不存在
+
曲线
凹
凹
由上表得:该函数无拐点。
例题4:函数f ( x ) = 1 x f(x)=\frac{1}{x} f ( x ) = x 1 f ′ ( x ) = − 1 x 2 f'(x)=-\frac{1}{x^2} f ′ ( x ) = − x 2 1 f ′ ′ ( x ) = 2 x 3 f''(x)=\frac{2}{x^3} f ′ ′ ( x ) = x 3 2 f ′ ′ ( x ) = 0 f''(x)=0 f ′ ′ ( x ) = 0 拐点一定是f ′ ( x ) = 0 f'(x)=0 f ′ ( x ) = 0 ( x ) ′ ′ (x)'' ( x ) ′ ′ f ( x ) ′ ′ f(x)'' f ( x ) ′ ′
函数的极值和最值问题 一个区域内,最值 只有1个,极值 可以有多个;局部区域内的最值 ;不可在端点处取得 ,只能在区域内部 取得。
极值定理f ( x ) f(x) f ( x ) x 0 x_0 x 0 f ′ ( x 0 ) = 0 f'(x_0)=0 f ′ ( x 0 ) = 0 极值+可导—>驻点 )。f ( x ) f(x) f ( x ) x 0 x_0 x 0 x 0 x_0 x 0 x 0 x_0 x 0 f ′ ( x ) > 0 f'(x)>0 f ′ ( x ) > 0 f ′ ( x ) < 0 f'(x)<0 f ′ ( x ) < 0 f ( x ) f(x) f ( x ) x 0 x_0 x 0 左增右减—>极大值 );x 0 x_0 x 0 f ′ ( x ) < 0 f'(x)<0 f ′ ( x ) < 0 f ′ ( x ) > 0 f'(x)>0 f ′ ( x ) > 0 f ( x ) f(x) f ( x ) x 0 x_0 x 0 左减右增—>极小值 );x 0 x_0 x 0 f ′ ( x ) f'(x) f ′ ( x ) f ( x ) f(x) f ( x ) x 0 x_0 x 0 左增右增/左减右减—>无极值 )。f ( x ) f(x) f ( x ) x 0 x_0 x 0 f ′ ( x 0 ) = 0 , f ′ ′ ( x 0 ) ≠ 0 f'(x_0)=0,f''(x_0)\ne 0 f ′ ( x 0 ) = 0 , f ′ ′ ( x 0 ) = 0 f ′ ′ ( x 0 ) < 0 f''(x_0)<0 f ′ ′ ( x 0 ) < 0 f ( x ) f(x) f ( x ) x 0 x_0 x 0 驻点+凸—>极大值 );f ′ ′ ( x 0 ) > 0 f''(x_0)>0 f ′ ′ ( x 0 ) > 0 f ( x ) f(x) f ( x ) x 0 x_0 x 0 驻点+凹—>极小值 );因为极值也可能在不可导点处取得,所以只能正推不能反推,即不是充要条件。 f ( x ) f(x) f ( x ) f ′ ( x ) f'(x) f ′ ( x ) f ′ ( x ) = 0 f'(x)=0 f ′ ( x ) = 0 f ′ ( x ) f'(x) f ′ ( x ) f ′ ( x ) f'(x) f ′ ( x ) f ′ ( x ) f'(x) f ′ ( x ) f ′ ( x ) = 0 f'(x)=0 f ′ ( x ) = 0 f ′ ′ ( x ) f''(x) f ′ ′ ( x ) f ( x ) = 2 x 3 − 6 x 2 − 18 x − 7 f(x)=2x^3-6x^2-18x-7 f ( x ) = 2 x 3 − 6 x 2 − 1 8 x − 7 ( − ∞ , + ∞ ) (-\infty,+\infty) ( − ∞ , + ∞ ) f ′ ( x ) = 6 x 2 − 12 x − 18 f'(x)=6x^2-12x-18 f ′ ( x ) = 6 x 2 − 1 2 x − 1 8 f ′ ( x ) = 0 f'(x)=0 f ′ ( x ) = 0 x 1 = − 1 , x 2 = 3 x_1=-1,x_2=3 x 1 = − 1 , x 2 = 3 f ′ ′ ( x ) = 12 x − 12 f''(x)=12x-12 f ′ ′ ( x ) = 1 2 x − 1 2 x = − 1 x=-1 x = − 1 f ′ ′ ( − 1 ) = − 24 < 0 f''(-1)=-24<0 f ′ ′ ( − 1 ) = − 2 4 < 0 x = − 1 x=-1 x = − 1 f ( − 1 ) = 2 ⋅ ( − 1 ) 3 − 6 ⋅ ( − 1 ) 2 − 18 ⋅ ( − 1 ) − 7 = 3 f(-1)=2 \cdot (-1)^3-6 \cdot (-1)^2-18 \cdot(-1) -7=3 f ( − 1 ) = 2 ⋅ ( − 1 ) 3 − 6 ⋅ ( − 1 ) 2 − 1 8 ⋅ ( − 1 ) − 7 = 3 x = 3 x=3 x = 3 f ′ ′ ( x ) 24 > 0 f''(x)24>0 f ′ ′ ( x ) 2 4 > 0 x = 3 x=3 x = 3 f ( 3 ) = 2 ⋅ 3 3 − 6 ⋅ 3 2 − 18 ⋅ 3 − 7 = 54 − 54 − 54 − 7 = − 61 f(3)=2 \cdot 3^3-6 \cdot 3^2-18 \cdot 3-7=54-54-54-7=-61 f ( 3 ) = 2 ⋅ 3 3 − 6 ⋅ 3 2 − 1 8 ⋅ 3 − 7 = 5 4 − 5 4 − 5 4 − 7 = − 6 1 f ( x ) = x − 3 2 x 2 3 + 1 2 f(x)=x-\frac{3}{2}x^{\frac{2}{3} }+\frac{1}{2} f ( x ) = x − 2 3 x 3 2 + 2 1 ( − ∞ , + ∞ ) (-\infty,+\infty) ( − ∞ , + ∞ ) f ′ ( x ) = 1 − x − 1 3 f'(x)=1-x^{-\frac{1}{3} } f ′ ( x ) = 1 − x − 3 1 f ′ ( x ) = 0 f'(x)=0 f ′ ( x ) = 0 x = 1 x=1 x = 1 x = 0 x=0 x = 0 1 − 1 x 3 1-\frac{1}{\sqrt[3]{x} } 1 − 3 x 1
(-∞,0)
0
(0,1)
1
(1,+∞)
f’(x)
+
×
-
0
+
f(x)
↗ \nearrow ↗ 极大
↘ \searrow ↘ 极小
↗ \nearrow ↗
由上表可知,当x = 0 x=0 x = 0 f ( 0 ) = 1 2 f(0)=\frac{1}{2} f ( 0 ) = 2 1 x = 1 x=1 x = 1 f ( 1 ) = 0 f(1)=0 f ( 1 ) = 0
最值f ′ ( x ) f'(x) f ′ ( x ) f ′ ( x ) = 0 f'(x)=0 f ′ ( x ) = 0 f ′ ( x ) f'(x) f ′ ( x ) f ( x ) = x − 3 2 x 2 3 + 1 2 f(x)=x-\frac{3}{2}x^{\frac{2}{3} }+\frac{1}{2} f ( x ) = x − 2 3 x 3 2 + 2 1 f ′ ( x ) = 1 − x − 1 3 f'(x)=1-x^{-\frac{1}{3} } f ′ ( x ) = 1 − x − 3 1 f ′ ( x ) = 0 f'(x)=0 f ′ ( x ) = 0 x = 1 x=1 x = 1 x = 0 x=0 x = 0 f ( 1 ) = 0 , f ( 0 ) = 1 2 , f ( − 1 ) = − 2 , f ( 8 ) = 5 2 f(1)=0,f(0)=\frac{1}{2},f(-1)=-2,f(8)=\frac{5}{2} f ( 1 ) = 0 , f ( 0 ) = 2 1 , f ( − 1 ) = − 2 , f ( 8 ) = 2 5 f ( 8 ) = 5 2 f(8)=\frac{5}{2} f ( 8 ) = 2 5 f ( − 1 ) = − 2 f(-1)=-2 f ( − 1 ) = − 2 y y y x x x
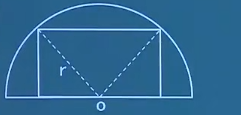
例题1:如图:在半径为r r r y y y x x x r 2 − ( x 2 ) 2 \sqrt{r^2-(\frac{x}{2})^2 } r 2 − ( 2 x ) 2 y = x ⋅ r 2 − ( x 2 ) 2 y=x \cdot \sqrt{r^2-(\frac{x}{2})^2 } y = x ⋅ r 2 − ( 2 x ) 2 y = r 2 ⋅ x 2 − 1 4 x 4 y=\sqrt{r^2\cdot x^2-\frac{1}{4}x^4 } y = r 2 ⋅ x 2 − 4 1 x 4 y ′ = 1 4 ⋅ z r 2 x − x 3 r 2 x 2 − 1 4 x 4 y'=\frac{1}{4}\cdot \frac{zr^2x-x^3}{\sqrt{r^2x^2-\frac{1}{4}x^4 } } y ′ = 4 1 ⋅ r 2 x 2 − 4 1 x 4 z r 2 x − x 3 x = 2 3 r x=\frac{2}{\sqrt{3} }r x = 3 2 r y ′ = 0 y'=0 y ′ = 0 x = 2 r x=\sqrt{2}r x = 2 r ∴ \therefore ∴ x = 2 r x=\sqrt{2}r x = 2 r 2 2 r \frac{\sqrt{2} }{2}r 2 2 r
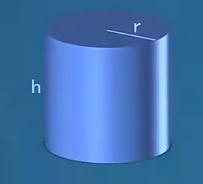
例题2:如图,需要造圆柱形油罐,体积为V V V r r r h h h y y y r r r V π r 2 \frac{V}{\pi r^2} π r 2 V y = 2 π r 2 + 2 V r y=2\pi r^2+\frac{2V}{r} y = 2 π r 2 + r 2 V y ′ = 4 π r − 2 V r 2 y'=4\pi r-\frac{2V}{r^2} y ′ = 4 π r − r 2 2 V y ′ = 0 y'=0 y ′ = 0 r = V 2 π 3 r=\sqrt[3]{\frac{V}{2\pi } } r = 3 2 π V r 3 = V 2 π = V = r 3 ⋅ 2 π r^3=\frac{V}{2 \pi} = V=r^3 \cdot 2\pi r 3 = 2 π V = V = r 3 ⋅ 2 π h = V π r 2 = r 3 ⋅ 2 π π r 2 = 2 r = 2 V 2 π 3 h=\frac{V}{\pi r^2}=\frac{r^3 \cdot 2\pi}{\pi r^2}=2r=2\sqrt[3]{\frac{V}{2\pi}} h = π r 2 V = π r 2 r 3 ⋅ 2 π = 2 r = 2 3 2 π V ∵ \because ∵ ∴ \therefore ∴ r = V 2 π 3 , h = 2 V 2 π 3 r=\sqrt[3]{\frac{V}{2\pi} },h=2\sqrt[3]{\frac{V}{2\pi}} r = 3 2 π V , h = 2 3 2 π V 2 r h = 1 1 \frac{2r}{h}=\frac{1}{1} h 2 r = 1 1
函数曲线的渐近线 曲线上的一动点,沿着曲线趋近于无穷远 时,该点与某直线的距离趋近于零 ,则称此直线为曲线的渐近线。斜渐近线:如果渐近线是斜的,称为斜渐近线。
水平渐近线x → ∞ x \to \infty x → ∞ x → + ∞ x \to +\infty x → + ∞ x → − ∞ x \to -\infty x → − ∞ " y = A " "y=A" " y = A "
垂直渐近线x 0 x_0 x 0 x → x 0 x \to x_0 x → x 0 x → x 0 + x \to x_0^+ x → x 0 + x → x 0 − x \to x_0^- x → x 0 − ∞ \infty ∞ " x = x 0 " "x=x_0" " x = x 0 "
斜渐近线曲线的渐近线可能有多条,也可能不存在 。y = 3 x 2 + 1 x 2 + 2 x − 3 y=\frac{3x^2+1}{x^2+2x-3} y = x 2 + 2 x − 3 3 x 2 + 1 lim x → ∞ 3 x 2 + 1 x 2 + 2 x − 3 = 3 \lim_{x \to \infty} \frac{3x^2+1}{x^2+2x-3} =3 lim x → ∞ x 2 + 2 x − 3 3 x 2 + 1 = 3 y = 3 y=3 y = 3 ∵ x 2 + 2 x − 3 ≠ 0 \because x^2+2x-3 \ne 0 ∵ x 2 + 2 x − 3 = 0 ∴ \therefore ∴ x = − 3 , x = 1 x=-3,x=1 x = − 3 , x = 1 ∵ lim x → − 3 3 x 2 + 1 x 2 + 2 x − 3 = ∞ \because \lim_{x \to -3} \frac{3x^2+1}{x^2+2x-3}=\infty ∵ lim x → − 3 x 2 + 2 x − 3 3 x 2 + 1 = ∞ ∵ lim x → 1 3 x 2 + 1 x 2 + 2 x − 3 = ∞ \because \lim_{x \to 1} \frac{3x^2+1}{x^2+2x-3}=\infty ∵ lim x → 1 x 2 + 2 x − 3 3 x 2 + 1 = ∞ ∴ \therefore ∴ x = − 3 , x = 1 x=-3,x=1 x = − 3 , x = 1 y = e x − 1 x y=\frac{e^x-1}{x} y = x e x − 1 lim x → − ∞ e x − 1 x = − 1 − ∞ = 0 \lim_{x \to -\infty} \frac{e^x-1}{x}=\frac{-1}{-\infty}=0 lim x → − ∞ x e x − 1 = − ∞ − 1 = 0 y = 0 y=0 y = 0 lim x → + ∞ e x − 1 x = + ∞ \lim_{x \to +\infty} \frac{e^x-1}{x}=+\infty lim x → + ∞ x e x − 1 = + ∞ e x − 1 x \frac{e^x-1}{x} x e x − 1 x ≠ 0 x \ne 0 x = 0 lim x → 0 e x − 1 x = 1 \lim_{x \to 0} \frac{e^x-1}{x}=1 lim x → 0 x e x − 1 = 1
导数习题 例题1. 曲线x y + e y 2 − x = 0 xy+e^{y^2}-x=0 x y + e y 2 − x = 0 ( 1 , 0 ) (1,0) ( 1 , 0 ) y = x − 1 y=x-1 y = x − 1 y + x y ′ + e y 2 ⋅ 2 y ⋅ y ′ − 1 = 0 y+xy'+e^{y^2} \cdot 2y \cdot y'-1=0 y + x y ′ + e y 2 ⋅ 2 y ⋅ y ′ − 1 = 0 y ′ = − 1 − y x + e y 2 ⋅ 2 y y'=-\frac{1-y}{x+e^{y^2}\cdot 2y} y ′ = − x + e y 2 ⋅ 2 y 1 − y y ′ ∣ ( 1 , 0 ) = 1 − 0 1 + 0 = 1 y'|(1,0)=\frac{1-0}{1+0}=1 y ′ ∣ ( 1 , 0 ) = 1 + 0 1 − 0 = 1 y − 0 = 1 ( x − 1 ) y-0=1(x-1) y − 0 = 1 ( x − 1 ) y = x − 1 y=x-1 y = x − 1 f ( x ) = e x 2 f(x)=e^{x^2} f ( x ) = e x 2 ( − ∞ , + ∞ ) (-\infty,+\infty) ( − ∞ , + ∞ ) f ′ ( x ) = 2 x e x 2 f'(x)=2xe^{x^2} f ′ ( x ) = 2 x e x 2 f ′ ( x ) = 0 f'(x)=0 f ′ ( x ) = 0 x = 0 x=0 x = 0 f ′ ′ ( x ) = 2 e x 2 + 4 x 2 e x 2 f''(x)=2e^{x^2}+4x^2e^{x^2} f ′ ′ ( x ) = 2 e x 2 + 4 x 2 e x 2
(-∞,0)
0
(0,+∞)
f’(x)
-
0
+
f(x)
↘ \searrow ↘ 极小
↗ \nearrow ↗
由上表可知,函数在( − ∞ , 0 ) (-\infty,0) ( − ∞ , 0 ) ( 0 , + ∞ ) (0,+\infty) ( 0 , + ∞ ) x = 0 x=0 x = 0 f ( x ) = e 0 = 1 f(x)=e^0=1 f ( x ) = e 0 = 1
例题3. 证明x > 0 x>0 x > 0 1 + 1 2 x > 1 + x 1+\frac{1}{2}x>\sqrt{1+x} 1 + 2 1 x > 1 + x F ( x ) = 1 + 1 2 x − 1 + x F(x)=1+\frac{1}{2}x-\sqrt{1+x} F ( x ) = 1 + 2 1 x − 1 + x F ′ ( x ) = 1 2 − 1 2 1 + x = 1 + x − 1 2 1 + x F'(x)=\frac{1}{2}-\frac{1}{2\sqrt{1+x} }=\frac{\sqrt{1+x}-1 }{2\sqrt{1+x} } F ′ ( x ) = 2 1 − 2 1 + x 1 = 2 1 + x 1 + x − 1 x > 0 x>0 x > 0 F ′ ( x ) > 0 F'(x)>0 F ′ ( x ) > 0 ∵ F ( x ) \because F(x) ∵ F ( x ) [ 0 , + ∞ ) [0,+\infty) [ 0 , + ∞ ) ∴ \therefore ∴ x > 0 x>0 x > 0 F ( x ) > F ( 0 ) = 0 F(x)>F(0)=0 F ( x ) > F ( 0 ) = 0 1 + 1 2 x − 1 + x > 0 1+\frac{1}{2}x-\sqrt{1+x}>0 1 + 2 1 x − 1 + x > 0 1 + 1 2 x > 1 + x 1+\frac{1}{2}x>\sqrt{1+x} 1 + 2 1 x > 1 + x f ( x ) = l n 1 + x 2 f(x)=ln1+x^2 f ( x ) = l n 1 + x 2 ( − ∞ , − 1 ) (-\infty,-1) ( − ∞ , − 1 ) ( − 1 , 1 ) (-1,1) ( − 1 , 1 ) ( 1 , + ∞ ) (1,+\infty) ( 1 , + ∞ ) ( − ∞ , − 1 ) , ( 1 , + ∞ ) (-\infty,-1),(1,+\infty) ( − ∞ , − 1 ) , ( 1 , + ∞ ) ( − ∞ , + ∞ ) (-\infty,+\infty) ( − ∞ , + ∞ ) f ′ ( x ) = 2 x 1 + x 2 f'(x)=\frac{2x}{1+x^2} f ′ ( x ) = 1 + x 2 2 x f ′ ′ ( x ) = 2 ⋅ ( 1 + x 2 ) − 2 x ⋅ 2 x ( 1 + x 2 ) 2 = 2 − 2 x 2 ( 1 + x 2 ) 2 f''(x)=\frac{2\cdot (1+x^2)-2x\cdot 2x}{(1+x^2)^2}=\frac{2-2x^2}{(1+x^2)^2} f ′ ′ ( x ) = ( 1 + x 2 ) 2 2 ⋅ ( 1 + x 2 ) − 2 x ⋅ 2 x = ( 1 + x 2 ) 2 2 − 2 x 2 f ′ ′ ( x ) = 0 f''(x)=0 f ′ ′ ( x ) = 0 x = − 1 x=-1 x = − 1 x = 1 x=1 x = 1
(-∞,-1)
-1
(-1,1)
1
(1,+∞)
f’(x)
-
0
+
0
-
曲线
凸
凹
凸
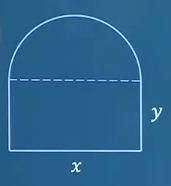
例题5. 某地区防空洞的截面拟建成矩形加半圆,截面的面积为5 m 2 5m^2 5 m 2 x x x L L L L = x + 2 y + π x 2 L=x+2y+\frac{\pi x}{2} L = x + 2 y + 2 π x 5 m 2 5m^2 5 m 2 5 = x y + 1 8 π x 2 5=xy+\frac{1}{8}\pi x^2 5 = x y + 8 1 π x 2 y = 5 − 1 8 π x 2 x = 5 x − π x 8 y=\frac{5-\frac{1}{8}\pi x^2}{x}=\frac{5}{x}-\frac{\pi x}{8} y = x 5 − 8 1 π x 2 = x 5 − 8 π x L = x + 2 ( 5 x − π x 8 ) + π x 2 = x + π 4 x + 10 x L=x+2(\frac{5}{x}-\frac{\pi x}{8})+\frac{\pi x}{2}=x+\frac{\pi }{4}x+\frac{10}{x} L = x + 2 ( x 5 − 8 π x ) + 2 π x = x + 4 π x + x 1 0 L ′ = 1 + π 4 − 10 x 2 L'=1+\frac{\pi }{4}-\frac{10}{x^2} L ′ = 1 + 4 π − x 2 1 0 L ′ = 0 L'=0 L ′ = 0 x = 40 4 + π x=\sqrt{\frac{40}{4+\pi } } x = 4 + π 4 0 ∵ \because ∵ ∴ \therefore ∴ x = 40 4 + π x=\sqrt{\frac{40}{4+\pi } } x = 4 + π 4 0 L L L ∴ \therefore ∴ x = 40 4 + π x=\sqrt{\frac{40}{4+\pi } } x = 4 + π 4 0 ∴ \therefore ∴ x = 40 4 + π x=\sqrt{\frac{40}{4+\pi } } x = 4 + π 4 0